Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
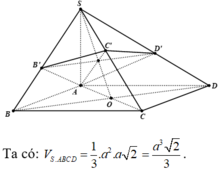
Dựa vào giả thiết ta có B', C', D' lần lượt là hình chiếu của A lên SB, SC, SD.
Tam giác SAC vuông cân tại A nên C' là trung điểm của SC.
Trong tam giác vuông SAB' ta có:
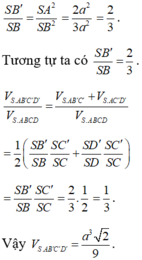


Chọn A
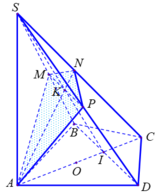
Gọi O là trọng tâm tam giác đều ABD và I là trung điểm BD thì:

Tam giác ICD vuông I có
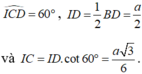
=> O và C đối xứng nhau qua đường thẳng BD

Tam giác SAC vuông tại A có SN. SC=SA²

Tam giác ABC có 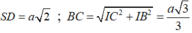 và AC²=AB²+BC²
và AC²=AB²+BC²
=> tam giác ABC vuông tại B ![]()
Lại có tam giác SAB vuông nên ![]() M là trung điểm SB
M là trung điểm SB
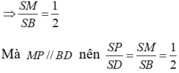
Mặt khác
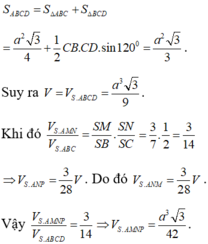

Chọn C.
Dễ thấy BD ⊥ SC, nên BD // (AB'C'D'), suy ra BD // B'D'.
Gọi I = AC ∩ BD, J = AC' ∩ SI, khi đó J là trọng tâm của tam giác SAC và J ∈ B'D'.
Suy ra
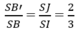
Do đó dễ thấy
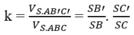

Chọn B

Ta có B C ⊥ S M . Gọi H là hình chiếu vuông góc của A trên SM. Do
![]() và FE đi qua H.
và FE đi qua H.
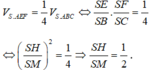
Vậy H là trung điểm cạnh SM. Suy ra tam giác SAM vuông cân tại A
⇒ S A = a 3 2 V S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8

Chọn D

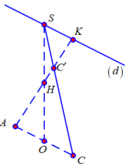
Gọi O là giao điểm của hai đường chéo AC và BD thì SO ∩ DD' = H. Khi đó H là trung điểm của SO và C' = AH ∩ SO.
Trong mặt phẳng (SAC) : Ta kẻ d // AC và AC' cắt (d) tại K. Khi đó áp dụng tính đồng dạng của các tam giác ta có:
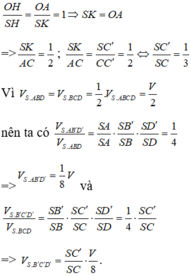
Suy ra:
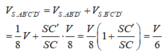
Lưu ý: Có thể sử dụng nhanh công thức:
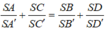

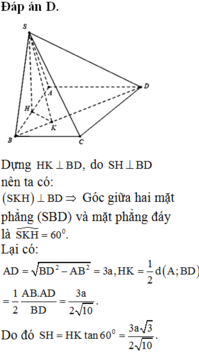
Chọn D
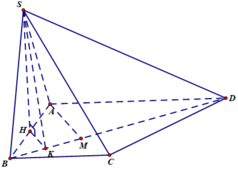
Ta có ![]()
Gọi H là trung điểm AB thì ![]() ,
,
kẻ ![]() , ta có
, ta có ![]() là góc giữa (SBD) và (ABCD), do đó
là góc giữa (SBD) và (ABCD), do đó ![]() = 600
= 600
Gọi AM là đường cao của tam giác vuông ABD. Khi đó, ta có:
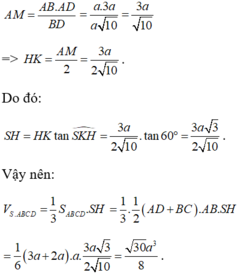

Chọn D.
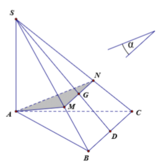
Do ( α ) đi qua G ∈ (SBC), song song với BC nên ( α ) cắt mặt phẳng (SBC) theo giao tuyến MN qua G và song song với BC.
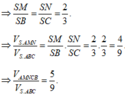
Do tam giác ABC vuông cân tại B, AC = a
2
nên ![]()
Do SA
⊥
(ABC) nên ![]()
![]()
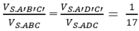
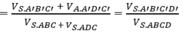
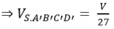
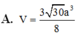
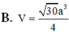
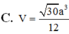
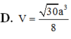
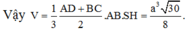
Chọn A.
Gọi K là trung điểm của AB.
DC//AB => DC//(SAB)=> DC//MN
Do đó