Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A.
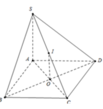
Do ABCD là hình chữ nhật nên khối cầu ngoại tiếp hình chóp S.BCD chính là khối cầu ngoại tiếp hình chóp S.ABCD
Khi đó
R = S C 2 = S A 2 + A B 2 + A D 2 2 = a 5 2 ⇒ V = 4 3 π R 3 = 5 π a 3 5 6
Đáp án A
Gọi O là giao điểm của 2 đường chéo AC và BIÊN ĐỘ, từ O dựng đường thẳng song song với SA và cắt SC tại trung điểm I của SC, suy ra I là tâm của mặt cầu ngoại tiếp hình chóp S.BCD
Mặt khác O I = 1 2 S A = a 2 O C = 1 2 A C = 1 2 a 2 + a 3 2 = a
Theo bài ra ta có: R = I C = O C 2 + O I 2 = a 5 2
Vậy thể tích khối cầu là V = 4 3 π a 5 2 3 = 5 π a 3 5 6
Đáp án C
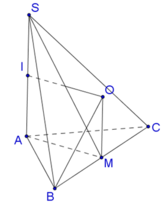
Gọi M là trung điểm của BC. Trong mặt phẳng (SAM), kẻ đường trung trực của đoạn thẳng SA , qua điểm M kẻ đường thẳng song song với SA , hai đường thẳng đó cắt nhau tại O .
Dễ dàng chứng minh được O là tâm mặt cầu ngoại tiếp chóp S.ABC .
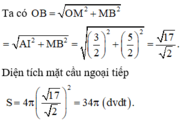
Đáp án A
Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD là R A B C D = A C 2 = a
Vậy bán kính mặt cầu ngoại tiếp khối chóp S.ABCD là
Đáp án A
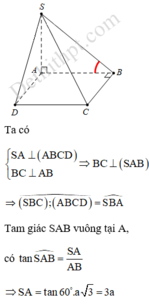
Ta có:
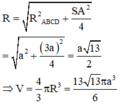
S A ⊥ A B C D B C ⊥ A B ⇒ B C ⊥ S A B ⇒ S B C ; A B C D ^ = S B A ^ R A B C D = A C 2 a .
Tam giác SAB vuông tại A, có
tan S B A ^ = S A A B ⇒ S A = tan 60 ∘ . a 3 = 3 a .
Bán kính đường tròn ngoại tiếp hình chữ nhật ABCD là
Vậy bán kính mặt cầu ngoại tiếp khối chóp S.ABCD là:
R = R A B C D 2 + S A 2 4 = a 2 + 3 a 2 4 = a 13 2 ⇒ V = 4 3 π R 3 = 13 13 π a 3 6
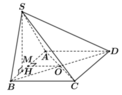
Gọi M là trung điểm AB, do tam giác SAB vuông tại S nên MS = MA = MB
Gọi H là hình chiếu của S trên AB. Từ giả thiết suy ra 
Ta có 
nên là trục của tam giác SAB, suy ra OA = OB = OS (2)
Từ (1) và (2) ta có OS = OA = OB = OC = OD.
Vậy O là tâm mặt cầu ngoại tiếp khối chóp S.ABCD bán kính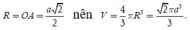 
Chọn B.
Đáp án D
Gọi O là tâm của hình chữ nhật ABCD và I là trung điểm của SC. Khi đó O I ⊥ ( A B C D )
⇒ I A = I B = I C = I D mà ∆ S A C vuông tại A I A = I S = I C . Do đó I là tâm mặt cầu ngoại tiếp khối chóp S.ABCD suy ra I A = a 2 ⇒ S C = 2 a 2 . Mặt khác AC là hình chiếu của SC trên mặt phẳng A B C D ⇒ S C ; A B C D ^ = S C ; A C ^ = S C A ^ = 45 ° .Suy ra ∆ S A C vuông cân ⇒ S A = A C = 2 a ⇒ V S . A B C D = 1 3 . S A . S A B C D = 1 3 . 2 a . a . a 3 = 2 a 3 3 3 .
Chọn đáp án A