Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

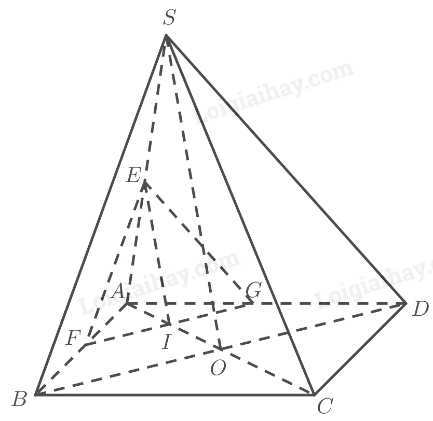
a) \(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\(M\) là trung điểm của \(SA\)
\( \Rightarrow OM\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OM\parallel SC\\SC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow OM\parallel \left( {SBC} \right)\)
\(O\) là trung điểm của \(B{\rm{D}}\) (theo tính chất hình bình hành)
\(N\) là trung điểm của \(SD\)
\( \Rightarrow ON\) là đường trung bình của tam giác \(SB{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow ON\parallel SB\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow ON\parallel \left( {SBC} \right)\)
\(\left. \begin{array}{l}OM\parallel \left( {SBC} \right)\\ON\parallel \left( {SBC} \right)\\OM,ON \subset \left( {OMN} \right)\end{array} \right\} \Rightarrow \left( {OMN} \right)\parallel \left( {SBC} \right)\)
b) \(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\(E\) là trung điểm của \(AB\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(ABC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow OE\parallel \left( {SBC} \right)\)
Do \(\left( {OMN} \right)\parallel \left( {SBC} \right)\) nên \(E \in \left( {OMN} \right)\)
Ta có:
\(\left. \begin{array}{l}EF \subset \left( {OMN} \right)\\\left( {OMN} \right)\parallel \left( {SBC} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {SBC} \right)\)

Qua S kẻ đường thẳng d song song AD (và BC)
Do \(\left\{{}\begin{matrix}S\in\left(SAD\right)\cap\left(SBC\right)\\AD||BC\\AD\in\left(SAD\right)\\BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\) giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song AD, BC
\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)

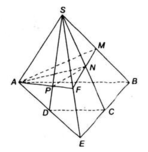
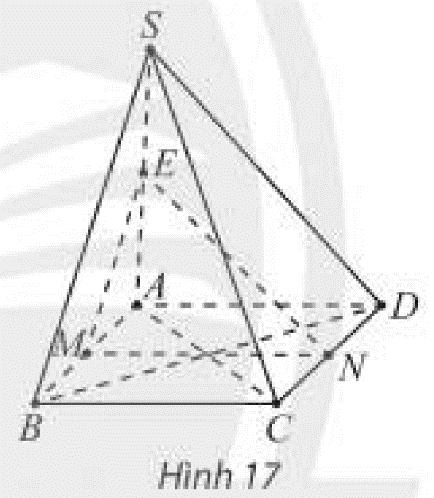
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
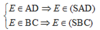
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.

Tham khảo hình vẽ:

a) • Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {IC{\rm{D}}} \right)\\M \in SA \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow M \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\\C \in \left( {IC{\rm{D}}} \right) \cap \left( {SAC} \right)\end{array}\)
\( \Rightarrow M,I,C\) thẳng hàng.
Do đó \(M\) là giao điểm của \(IC\) và \(SA\).
• Ta có:
\(\begin{array}{l}\left. \begin{array}{l}N \in \left( {IC{\rm{D}}} \right)\\N \in SB \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow N \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\\left. \begin{array}{l}I \in \left( {IC{\rm{D}}} \right)\\I \in SO \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\\D \in \left( {IC{\rm{D}}} \right) \cap \left( {SB{\rm{D}}} \right)\end{array}\)
\( \Rightarrow N,I,D\) thẳng hàng.
Do đó \(N\) là giao điểm của \(I{\rm{D}}\) và \(SB\).
• Ta có:
\(\begin{array}{l}AB = \left( {SAB} \right) \cap \left( {ABC{\rm{D}}} \right)\\C{\rm{D}} = \left( {IC{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\MN = \left( {SAB} \right) \cap \left( {IC{\rm{D}}} \right)\\AB\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(AB\parallel C{\rm{D}}\parallel MN\).
Áp dụng định lí Medelaus cho tam giác \(SOA\) với cát tuyến \(CIM\), ta có:
\(\frac{{SM}}{{MA}}.\frac{{AC}}{{OC}}.\frac{{OI}}{{SI}} = 1 \Leftrightarrow \frac{{SM}}{{MA}}.2.1 = 1 \Leftrightarrow \frac{{SM}}{{MA}} = \frac{1}{2}\)
Xét tam giác \(SAB\) có \(MN\parallel AB\). Theo định lí Thales ta có:
\(\frac{{MN}}{{AB}} = \frac{{SM}}{{MA}} = \frac{1}{2} \Leftrightarrow MN = \frac{1}{2}AB = \frac{a}{2}\)
b) Ta có:
\(\begin{array}{l}BC = \left( {SBC} \right) \cap \left( {ABC{\rm{D}}} \right)\\A{\rm{D}} = \left( {SA{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right)\\SK = \left( {SAD} \right) \cap \left( {SBC} \right)\\AD\parallel BC\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(SK\parallel BC\parallel A{\rm{D}}\).

a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
TenAnh1 A = (-0.14, -7.4) A = (-0.14, -7.4) A = (-0.14, -7.4) B = (14.46, -7.36) B = (14.46, -7.36) B = (14.46, -7.36) C = (-3.74, -5.6) C = (-3.74, -5.6) C = (-3.74, -5.6) D = (11.62, -5.6) D = (11.62, -5.6) D = (11.62, -5.6)

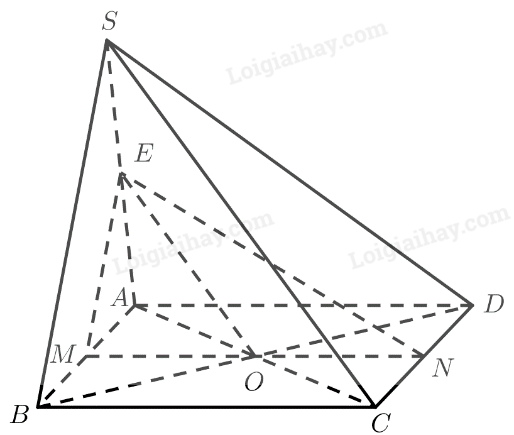
a) \(M\) là trung điểm của \(AB\)
\(N\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABCD\)
\( \Rightarrow MN\parallel A{\rm{D}}\parallel BC\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}MN\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SBC} \right)\\\left. \begin{array}{l}MN\parallel A{\rm{D}}\\A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SA{\rm{D}}} \right)\end{array}\)
b) \(M\) là trung điểm của \(AB\)
\(E\) là trung điểm của \(SA\)
\( \Rightarrow ME\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow ME\parallel SB\\ME \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SB\parallel \left( {MNE} \right)\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
\( \Rightarrow O\) là trung điểm của \(AC\) và \(O,M,N\) thẳng hàng
Mà \(E\) là trung điểm của \(SA\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel SC\\OE \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SC\parallel \left( {MNE} \right)\)

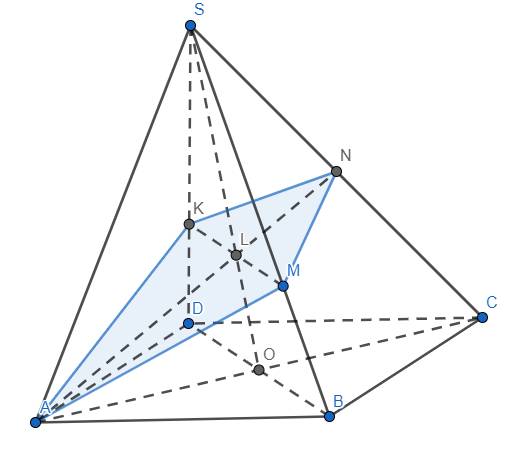
a) Gọi \(O=AC\cap BD\). Khi đó \(O\in\left(SAC\right)\cap\left(SBD\right)\). Lại có \(S\in\left(SAC\right)\cap\left(SBD\right)\) nên SO chính là giao tuyến của (SAC) và (SBD).
b) Trong mp (AMNK) cho \(AN\cap MK=L\). Do \(AN\subset\left(SAC\right),MK\subset\left(SBD\right)\) nên \(L\in\left(SAC\right)\cap\left(SBD\right)\) nên \(L\in SO\). \(\Rightarrow\) L là trọng tâm tam giác SAC \(\Rightarrow\dfrac{SL}{LO}=2\). Mà \(\dfrac{SM}{MB}=2\) nên \(\dfrac{SL}{LO}=\dfrac{SM}{MB}\Rightarrow\) LM//BO hay MK//BD, suy ra đpcm.

Ta có: Sx là giao tuyến (SAD) và (SBC) sao cho Sx // AD // BC (1)
Có : M, N là trung điểm của AB, CD
Suy ra: MN // AD // BC (2)
Từ (1)(2) suy ra: MN // Sx.

Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Ta có:
\(I\) là trung điểm của \(SD\)
\(O\) là trung điểm của \(BD\) (theo tính chất hình bình hành)
\( \Rightarrow OI\) là đường trung bình của tam giác \(SB{\rm{D}}\)
\( \Rightarrow OI\parallel SB\)
Ta có:
\(\begin{array}{l}Cx = \left( {IAC} \right) \cap \left( {SBC} \right)\\SB = \left( {SB{\rm{D}}} \right) \cap \left( {SBC} \right)\\OI = \left( {IAC} \right) \cap \left( {SB{\rm{D}}} \right)\\SB\parallel OI\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(OI\parallel SB\parallel Cx\).