Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong tam giác SBD, MN là đường trung bình \(\Rightarrow MN||BD\)
\(\Rightarrow MN||\left(ABCD\right)\)
Trong mp (ABCD), qua E kẻ đường thẳng song song BD cắt BC tại F và cắt AD kéo dài tại G
Trong mp (SAD), nối GN kéo dài cắt SA tại P
Ngũ giác PNEFM là thiết diện của (MNE) và chóp

Gọi P là giao điểm của mặt phẳng (EMN) với cạnh AB. Ta có ME là đường trung bình của tam giác SAB, nên ta có ME song song với đoạn thẳng AB và ME = 1/2 * AB. Tương tự, ta cũng có MN song song với cạnh SC và MN = 1/2 * SC. Vì EMN là tam giác đều, nên ta có EP = EN = NP = 1/3 * EMN.
Vì E là trung điểm của SA, nên ta có SE = 1/2 * SA. Vì SN là đường trung bình của tam giác SCA, nên ta có SN = 1/2 * SC.
Từ các thông tin trên, ta có thể xác định các điểm P, E, và N trên hình chóp S.ABCD. Sau đó, ta vẽ đường thẳng EN và vẽ đường thẳng qua P song song với đáy ABCD, giao điểm của hai đường thẳng này là điểm M.
Vậy, thiết diện của hình chóp S.ABCD khi cắt bởi mặt phẳng (EMN) là một hình bình hành có các đỉnh là các điểm E, M, N và các cạnh là các đoạn thẳng EM, MN, NE.

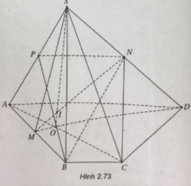
(h.2.73) a) Gọi O = AC ∩ MD Trong mặt phẳng (SMB) gọi I = SO ∩ MN.
Ta có: I = (SAC) ∩ MN
b) AD // BC (BC ⊂ (SBC))
⇒ AD // (SBC). Mặt phẳng (SAD) cắt mặt phẳng (NBC) theo giao tuyến NP // AD (P ∈ SA). Ta có thiết diện cần tìm là hình thang BCNP.

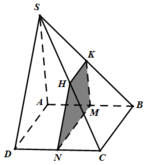

=> giao tuyến của (SCD) và (α) là NH// SD.
+ lại có HK là giao tuyến của (α) và (SBC) .
Thiết diện là tứ giác MNHK.
Ba mặt phẳng (ABCD) ; (SBC) và (α) đôi một cắt nhau theo các giao tuyến là MN; HK và BC mà MN// BC nên MN// HK. Vậy thiết diện là một hình thang .
Chọn B.

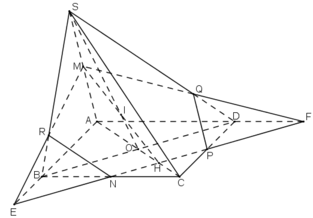
a) Tìm thiết diện :
Trong mp(ABCD), gọi F = AD ∩ PN và E = AB ∩ PN
Trong mp(SAD), gọi Q = MF ∩ SD
Trong mp(SAB), gọi R = ME ∩ SB
Nối PQ, NR ta được các đoạn giao tuyến của mp(MNP) với các mặt bên và mặt đáy của hình chóp là MQ, QP, PN, NR, RM
Vậy thiết diện cắt bởi mặt phẳng (MNP) là ngũ giác MQPNR.
b) Tìm SO ∩ (MNP). Gọi H là giao điểm của AC và PN .
Trong (SAC), SO ∩ MH = I
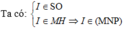
Vậy I = SO ∩ (MNP).

a, Mình nghĩ ý bạn là (MNP)
Trong (ABCD) gọi E = \(NP\cap BD\)
⇒ E ∈ (SBD)
Do K ∈ SD ⇒ K ∈ (SBD). M là trung điểm của SB ⇒ M ∈ (SBD)
Trong (SBD) gọi F = BK \(\cap\) ME
⇒ \(\left\{{}\begin{matrix}F\in BK\\F\in\left(MNP\right)\end{matrix}\right.\) ⇒ F = BK \(\cap\) (MNP)
b, Trong (ABCD) gọi O = AC \(\cap\) BD và H = BN \(\cap\) AC
Trong (SBD) gọi G = BK \(\cap\) SO
Trong (SAC) gọi I = SA \(\cap\) HG
(BNK) \(\cap\) (SAD) = IK
(BNK) \(\cap\) (SCD) = KN
(BNK) \(\cap\) (ABCD) = NB
(BNK) \(\cap\) (SAD) = BI
⇒ Thiết diện tạo bởi hình chóp S.ABCD và (BNK) là tứ giác IKNB

Trong mp (ABCD), nối MN kéo dài lần lượt cắt AD tại F và DC tại G
Trong mp (SAD), nối FE cắt SA tại P
Trong mp (SCD), nối EG cắt SC tại Q
\(\Rightarrow\) Ngũ giác MNQEP là thiết diện của (MNE) và chóp
Em cảm ơn ạ