Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

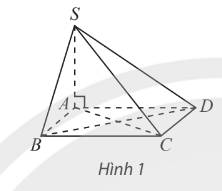
Ta có:\(SA\perp\left(ABCD\right)\Rightarrow SA\perp CD.\)
\(ABCD\) là hình vuông \(\Rightarrow CD\perp AD.\)
\(\Rightarrow CD\perp\left(SAD\right).\)
\(\Rightarrow A\)

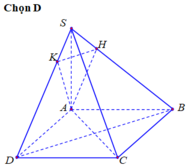
Phương án A sai vì AB và CB không vuông góc với giao tuyến SB của (SAB) và (SBC), nên góc ABC không phải là góc của hai mặt phẳng này; phương án B sai vì góc BAD không phải là góc của hai mặt phẳng (SAB) với mặt phẳng (SBC); phương án C sai vì AB ⊥ BC thì chưa đủ để kết luận AB vuông góc với mặt phẳng (SBC); phương án D đúng vì : BC ⊥ (SAB) do BC ⊥ AB và BC ⊥ SA ⇒ (SBC) ⊥ (SAB)
Đáp án D

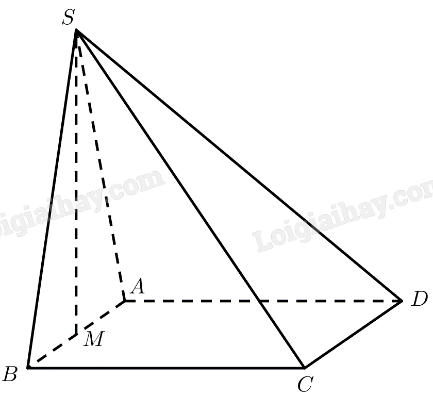
a, Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)
Tam giác \(SAB\) vuông cân tại \(S\), có \(M\) là trung điểm của \(AB\)
\(\left. \begin{array}{l} \Rightarrow SM \bot AB\\\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\end{array} \right\} \Rightarrow SM \bot \left( {ABCD} \right)\)
b) \(ABCD\) là hình chữ nhật \( \Rightarrow AB \bot A{\rm{D}}\)
\(SM \bot \left( {ABCD} \right) \Rightarrow SM \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\)
c) \(A{\rm{D}} \bot \left( {SAB} \right) \Rightarrow A{\rm{D}} \bot SB\)
Tam giác \(SAB\) vuông cân tại \(S\)\( \Rightarrow SA \bot SB\)
\(\left. \begin{array}{l} \Rightarrow SB \bot \left( {SA{\rm{D}}} \right)\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SA{\rm{D}}} \right)\)

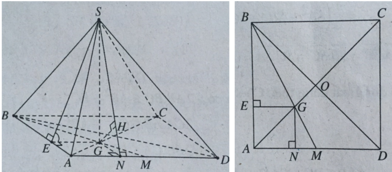
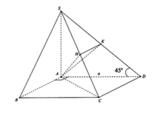
+ Xác định góc của (SAB) và mặt phẳng đáy.
Gọi G là trọng tâm tam giác ABD và E là hình chiếu của G lên AB. Ta có:
AB ⊥ SG & AB ⊥ GE⇒ AB ⊥ (SEG) ⇒ AB ⊥ SE.
SE ⊥ AB & GE ⊥ AB⇒ ∠((SAB),(ABCD)) = ∠(SEG) = 60o.
+ Xác định khoảng cách từ B đến mặt phẳng (SAD).
Hạ GN ⊥ AD. Tương tự như trên, ta có: AD ⊥ GN & AD ⊥ SG⇒ AD ⊥ (SGN)
Hạ GH ⊥ SN, ta có GH ⊥ (SAD) suy ra khoảng cách từ G đến (SAD) là GH.
+ Tính GH.
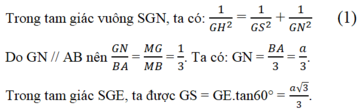
(do GE = GN). Thế vào (1) ta được:
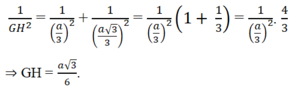
Ta có: M ∈(SAD) & MB = 3MG⇒ d(B,(SAD)) = 3d(G,(SAD)) = (a√3)/2.

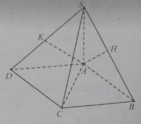
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)

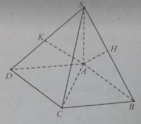
Phương án A sai vì hai điều kiện AH ⊥ (SBC) (do AH ⊥ SB và AH ⊥ BC) và AK ⊥ (SCD) (do AK vuông góc với SD và AK ⊥ CD) chưa liên quan đến (SAC); phương án B đúng vì AH ⊥(SBC) và AK ⊥ (SCD) nên SC ⊥ (AHK), từ đó suy ra hai mặt phẳng (AHK) và (SAC) vuông góc; phương án C và D đều sai vì chưa đủ điều kiện kết luận SC ⊥ (AHK)
Đáp án B