Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Kẻ C H ⊥ A B .
Bằng tính toán hình thang vuông thông thương ta có được:


Đáp án C.
Không mất tính tổng quát, giả sử a = 1
Xét hệ trục tọa độ Oxyz với
A 0 ; 0 ; 0 ; D 2 ; 0 ; 0 ;
B 0 ; 1 ; 0 ; S 0 ; 0 ; 5 .
Điểm C thỏa mãn
B C → = 1 2 A D → = 1 ; 0 ; 0
⇒ C 1 ; 1 ; 0 .
mp(SBC) có
n 1 → = S B → ; B C → = 0 ; 1 ; − 5 ; 1 ; 0 ; 0
= 0 ; − 5 ; − 1 .
mp(SCD) có
n 2 → = S D → ; C D → = 2 ; 0 ; − 5 ; 1 ; − 1 ; 0 = 5 ; 5 ; 2 .
Do đó côsin của góc tạo bởi hai mặt phẳng (SBC) và (SCD) bằng:
cos α = n 1 → . n 2 → n 1 . n 2 = 7 2 3 = 21 6 .
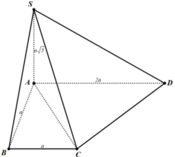

Đáp án D
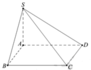
Hạ H, K lần lượt là hình chiếu vuông góc của A xuống SB và SD.
Ta có:
A H ⊥ S B A H ⊥ B C ⇒ A H ⊥ S B C . Tương tự A K ⊥ S D C
Như vậy S B C , S D C ^ = A H , A K ^ = H A K ^
Ta có Δ S A B = Δ S A D suy ra A H = A K . Vì góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 nên ΔAHK đều.
Ta có S H S B = S K S D = H K B D , mà S H S B = S A 2 S B 2 = x 2 x 2 + a 2 = K H a 2 suy ra K H = a 2 x 2 x 2 + a 2 .
Ta lại có 1 A H 2 = 1 S A 2 + 1 A B 2 = a 2 + x 2 a 2 x 2 suy ra A H 2 = a 2 x 2 a 2 + x 2 .
ΔAHK đều nên ta có
K H 2 = A H 2 ⇔ a 2 x 2 x 2 + a 2 2 = a 2 x 2 a 2 + x 2 ⇔ x = a .
Vậy x = a thì góc giữa hai mặt phẳng (SBC) và (SCD) bằng 60 0 .

Đáp án C
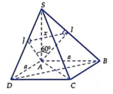
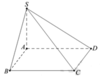
+ Trong S A B dựng A I ⊥ S B ta chứng minh được A I ⊥ S B C 1 .
Trong S A D dựng A J ⊥ S D ta chứng minh được A J ⊥ S C D 2 .
Từ (1) và (2) ⇒ S B C , S C D ^ = A I , A J ^ = I A J ^
+ Ta chứng minh được A I = A J . Do đó, nếu góc I A J ^ = 60 ° thì Δ A I J đều ⇒ A I = A J = I J .
Δ S A B vuông tại A có AI là đường cao ⇒ A I . S B = S A . A B ⇒ A I = S A . A B S B 3
Và có S A 2 = S I . S B ⇒ S I = S A 2 S B 4
Ta chứng minh được I J // B D ⇒ I J B D = S I S B ⇒ I J = S I . B D S B = 4 S A 2 . B D 2 S B 2 5 .
Thế (3)&(5) vào A I = I J ⇒ A B = S A . B D S B ⇔ A B . S B = S A . B D .
⇔ a . x 2 + a 2 = x . a 2 ⇔ x 2 + a 2 = 2 x 2 ⇔ x = a

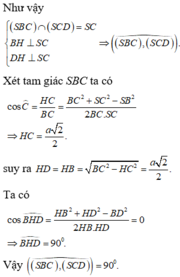
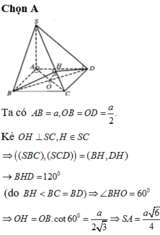
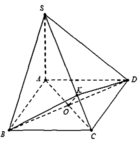

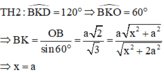

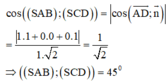

Gọi O là tâm hình vuông và H là hình chiếu của O lên SC
Ta có O H D ^ = 60 o ( D H B ^ là góc giữa hai mặt phẳng (SCD) và (SBC) )
Diện tích của ∆ S O C là
x a 2 2 = O H . S C ⇒ O H = x a 2 2 x 2 + 2 a a O H = a 2 2 . 1 3
Do đó x = a
Đáp án A