Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

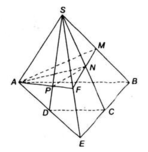
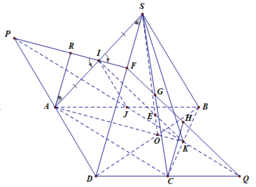
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
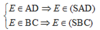
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.

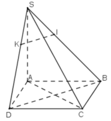
a) Để tìm giao điểm M của SD và (GHK), ta có thể sử dụng tính chất của đường thẳng và mặt phẳng. Đầu tiên, ta cần tìm phương trình đường thẳng SD và phương trình mặt phẳng GHK. Sau đó, ta giải hệ phương trình để tìm giao điểm M.
b) Để chứng minh G, E, M thẳng hàng, ta có thể sử dụng định lý về trọng tâm của tam giác và tính chất của trung điểm. Chúng ta cần chứng minh rằng G, E, M nằm trên cùng một đường thẳng.

a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP

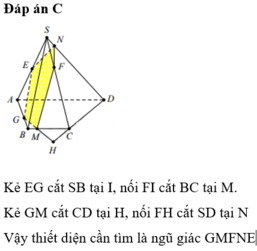
Qua G kẻ đường thẳng song song AC lần lượt cắt AD, AB, BC tại E, F, N.
là giao tuyến của (GHK) và (ABCD)
Nối EH kéo dài cắt SD tại M là giao điểm SD và (NHK)
c/ Gọi P là giao điểm của FN kéo dài và CD
Ta có , mà BD qua trung điểm của AC qua trung điểm của EP là trung điểm EP
Mà MG qua trung điểm của EP MG qua trung điểm của HK hay G,M,E thẳng hàng

a, đề là gì vậy bạn
b, Xét (ABCD) kẻ AI giao CD tại I
Xét (SCD); (KAG) có
K là điểm chung t1 ; I là điểm chung t2
=> KI là giao tuyến 2 mp
=> Nối IK cắt SD tại M
c, Ta có M = (SAIM) giao (GHK)
E = (HKAI) giao (GHK)
G = (HKAI) giao (SAIM)
mà ME ko song song vs MG
=> M;E;G thẳng hàng

a) Ta có:
\(SA \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SA \bot CB\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AB \bot CB\)
\( \Rightarrow CB \bot \left( {SAB} \right)\)
\(SA \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SA \bot CD\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AD \bot CD\)
\( \Rightarrow CD \bot \left( {SAD} \right)\)
b) Ta có:
\(\left. \begin{array}{l}CB \bot \left( {SAB} \right) \Rightarrow CB \bot AH\\AH \bot SB\end{array} \right\} \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow AH \bot SC\)
\(\left. \begin{array}{l}CD \bot \left( {SAD} \right) \Rightarrow CD \bot AK\\AK \bot SD\end{array} \right\} \Rightarrow AK \bot \left( {SC{\rm{D}}} \right) \Rightarrow AK \bot SC\)
\( \Rightarrow SC \bot \left( {AHK} \right) \Rightarrow SC \bot HK\)
\(\begin{array}{l}\Delta SAB = \Delta SA{\rm{D}}\left( {c.g.c} \right) \Rightarrow SH = SK,SB = S{\rm{D}}\\\left. \begin{array}{l} \Rightarrow \frac{{SH}}{{SB}} = \frac{{SK}}{{S{\rm{D}}}} \Rightarrow HK\parallel B{\rm{D}}\\SA \bot \left( {ABC{\rm{D}}} \right) \Rightarrow SA \bot B{\rm{D}}\end{array} \right\} \Rightarrow SA \bot HK\end{array}\)
\(\left. \begin{array}{l}SC \bot HK\\SA \bot HK\end{array} \right\} \Rightarrow HK \bot \left( {SAC} \right) \Rightarrow HK \bot AI\)