Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

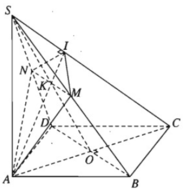
a) Gọi I là giao điểm của mặt phẳng (α) với cạnh SC. Ta có: (α) ⊥ SC, AI ⊂ (α) ⇒ SC ⊥ AI. Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và AI ⊂ (α), nên K là giao điểm của SO với (α).
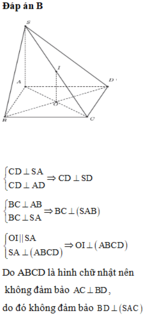
b) Ta có 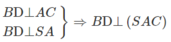
⇒ BD ⊥ SC
Mặt khác BD ⊂ (SBD) nên (SBD) ⊥ (SAC).
Vì BD ⊥ SC và (α) ⊥ SC nhưng BD không chứa trong (α) nên BD // (α)
Ta có K = SO ∩ (α) và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD).
Mặt phẳng (SBD) chứa BD // (α) nên cắt theo giao tuyến d // BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD).
Gọi M và N lần lượt là giao điểm của d với SB và SD. Ta được thiết diện là tứ giác AIMN vuông góc với SC và đường chéo MN song song với BD.

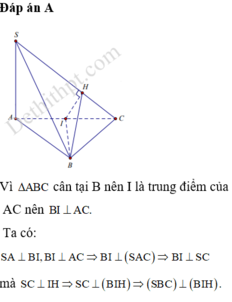
Chọn đáp án A
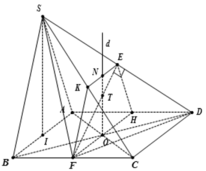
+ Gọi O là tâm của hình vuông ABCD. Qua O ta dựng đường thẳng d vuông góc với mặt đáy.
+ Gọi E, K, F, H, N lần lượt là trung điểm của các đoạn thẳng SD, SC, BC, AD, EK
+ Ta có tam giác SDF là tam giác cân tại F. Vì FD = FS = a 5 (độc giả tự chứng minh)
Suy ra FE ⊥ SD
Mặt khác, ta có KE // FH (Vì cùng song song với CD). Nên 4 điểm K, E, F, H đồng phẳng
+ Trong mặt phẳng (KEFH), gọi T là giao điểm của FE và ON.
Ta có T là tâm mặt cầu ngoại tiếp hình chóp S. ABCD
+ Ta có tam giác EKO là tam giác đều cạnh a. Nên
![]()
Bán kính mặt cầu là
![]()
+ Xét tam giác vuông TOB vuông tại B, ta có
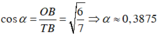

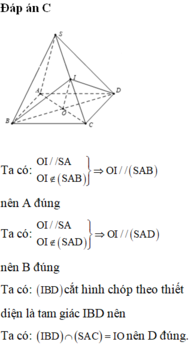
Chọn C.
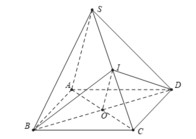
+) Ta có:
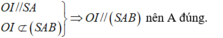
+) Ta có:
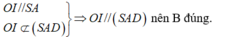
+) Ta có: mp (IBD) cắt hình chóp theo thiết diện là tam giác IBD nên C sai.
+) Ta có: (IBD) ∩ (SAC) = IO nên D đúng.
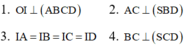
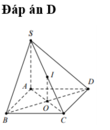



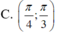
Đáp án A