Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) N trung điểm AD \(\Rightarrow AN=\frac{AD}{2}=\frac{BC}{2}\)
M trung điểm BC \(\Rightarrow MC=\frac{BC}{2}\Rightarrow AN=MC\)mà AN//MC
nên AMCN là hình bình hành \(\Rightarrow\overrightarrow{AM}=\overrightarrow{NC}\)
b) Tương tự câu a ta được \(\hept{\begin{cases}ND=BM=\frac{1}{2}BC\\ND//BM\end{cases}}\)=> NDMB là hình bình hành=> NB//DM (1)
Xét 2 tam giác ANI và NDK: \(\hept{\begin{cases}AN=ND=\frac{AD}{2}\\\widehat{NAI}=\widehat{DNK}\left(AM//NC\right)\\\widehat{ANI}=\widehat{NDK}\left(NB//MD\right)\end{cases}\Rightarrow\Delta ANI=\Delta NDK\left(g.c.g\right)}\)
\(\Rightarrow NI=DK\)(2)
(1), (2) => \(\overrightarrow{NI}=\overrightarrow{DK}\)

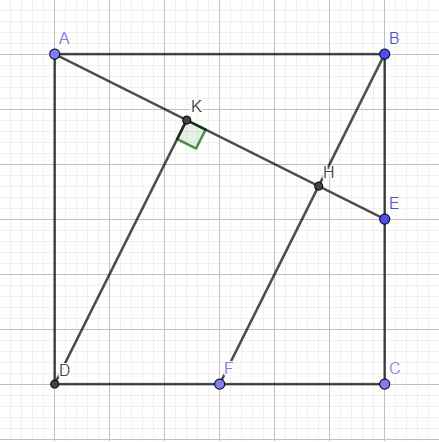
a. Dễ dàng chứng minh hai tam giác vuông ABE và BCF bằng nhau (c.g.c)
\(\Rightarrow\widehat{AEB}=\widehat{BFC}\)
Mà \(\widehat{AEB}+\widehat{AEC}=180^0\Rightarrow\widehat{BFC}+\widehat{AEC}=180^0\)
\(\Rightarrow\widehat{EHF}=360^0-\left(\widehat{C}+\widehat{BFC}+\widehat{AED}\right)=90^0\)
Hay \(AE\perp BF\)
b.
Áp dụng hệ thức lượng cho tam giác vuông ABE:
\(AB^2=AH.AE\Rightarrow AH=\dfrac{AB^2}{AE}\Rightarrow\dfrac{AH}{AE}=\dfrac{AB^2}{AE^2}=\dfrac{AB^2}{AB^2+BE^2}=\dfrac{AB^2}{AB^2+\left(\dfrac{AB}{2}\right)^2}=\dfrac{4}{5}\)
\(\dfrac{BH}{BF}=\dfrac{BH}{AE}=\dfrac{\dfrac{AB.BE}{AE}}{AE}=\dfrac{AB.BE}{AE^2}=\dfrac{AB.\dfrac{1}{2}AB}{AB^2+\left(\dfrac{1}{2}AB\right)^2}=\dfrac{2}{5}\)
c. Hai tam giác vuông ABH và DAK đồng dạng (\(\widehat{ADK}\) và \(\widehat{BAH}\) cùng phụ \(\widehat{DAK}\))
\(\Rightarrow\dfrac{AK}{AD}=\dfrac{BH}{AB}\Rightarrow AK=\dfrac{AD.BH}{AB}=BH\)
Mà \(tan\widehat{BAH}=\dfrac{BH}{AH}=\dfrac{BE}{AB}=\dfrac{1}{2}\Rightarrow BH=\dfrac{1}{2}AH\)
\(\Rightarrow AK=\dfrac{1}{2}AH\) hay K là trung điểm AH

Đáp án: B
a sai vì trực tâm là giao điểm của ba đường cao, không phải ba đường phân giác.
b sai vì hai đường chéo của hình bình hành không bằng nhau.
c, d, e đúng.
a: \(F\in SC\subset\left(SAC\right)\)
\(F\in\left(FBD\right)\)
Do đó: \(F\in\left(SAC\right)\cap\left(FBD\right)\)
Gọi O là giao điểm của AC và BD trong mp(ABCD)
=>\(O\in\left(SAC\right)\cap\left(FBD\right)\)
Do đó: \(\left(SAC\right)\cap\left(FBD\right)=FO\)
b: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
Thank you Nguyễn Lê Phước Thịnh nhé