Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tham khảo:
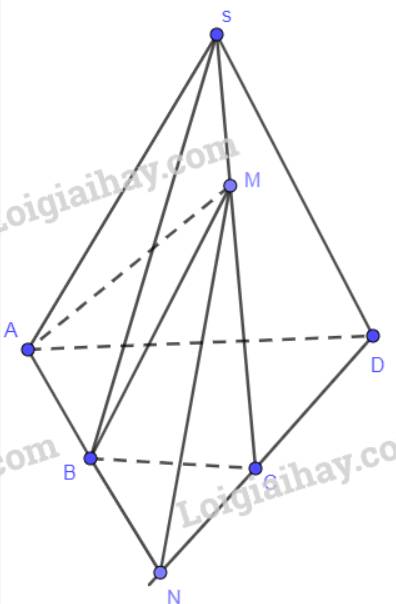
Ta có N thuộc đường thẳng AB , mà AB nằm trong mặt phẳng (ABM) nên N cũng nằm trong mp(ABM)
M và N đều nằm trong mặt phẳng (ABM) nên MN nằm trong mp(ABM) (1)
M thuộc SC suy ra M nằm trong mp(SCD), N thuộc đường thẳng CD nên N nằm trong mp(SCD)
Do đó, MN nằm trong mp(SCD) (2)
Từ (1) và (2) suy ra MN là giao tuyến của hai mp(ABM) và (SCD)
Tham khảo:
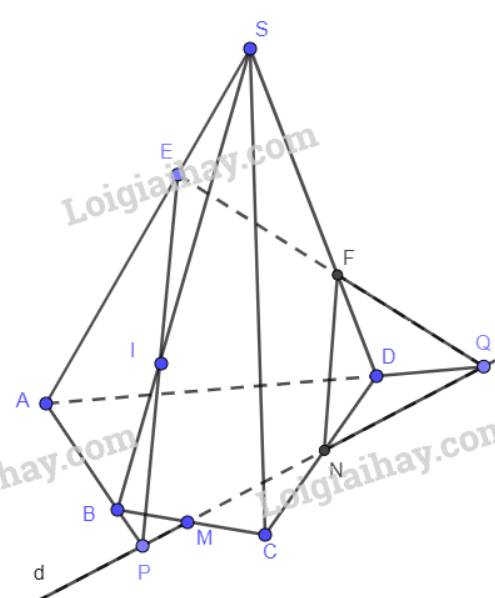
a)
- Giao điểm của mp(E,d) với cạnh SB
P thuộc AB suy ra P cũng thuộc mp(SAB)
Trên mp(SAB), gọi giao điểm của EP và SB là I
P thuộc đường thẳng d suy ra P cũng nằm trên mp(E,d)
E, P đều nằm trên mp(D,d) suy ra EP nằm trên mp(E,d) suy ra I cũng nằm trên mp(E,d)
Vậy I là giao điểm của mp(E,d) và SB
- Giao điểm của mp(E,d) với cạnh SD.
Q thuộc AD suy ra Q nằm trên mp(SAD)
Gọi giao điểm của EQ và SD là F
Q thuộc đường thẳng d suy ra Q cũng nằm trên mp(E,d)
E, Q đều nằm trên mp(E,d) suy ra EQ nằm trên mp(E,d) , suy ra F cũng nằm trên mp(E,d)
Vậy F là giao điểm của mp(E,d) và SD.
b) Ta có EI cùng thuộc mp(SAB) và mp(E,d) suy ra EI là tuyến điểm của hai mặt phẳng.
EF cùng thuộc mp(SAD) và mp(E,d) suy ra EF là giao tuyến của hai mặt phẳng
\(IM \subset mp\left( {SBC} \right),IM \subset mp\left( {E,d} \right)\) suy ra IM là giao tuyến của hai mp(SBC) và mp(E,d).
\(FN \subset mp\left( {SCD} \right),FN \subset mp\left( {E,d} \right)\) suy ra FN là giao tuyến của mp(SCD) và mp(E,d).
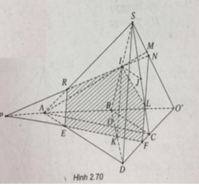
a) Gọi O′ = AB ∩ CD, M = AI ∩ SO′
Ta có: M = AI ∩ (SCD)
b) IJ // BC ⇒ IJ // AD ⇒ IJ // (SAD)
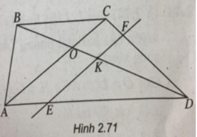
c) Đường thẳng qua I song song với SD cắt BD tại K.
Do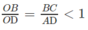 
nên OB < OD. Do đó điểm K thuộc đoạn OD.
Qua K, kẻ đường thẳng song song với AC cắt DA, DC, BA lần lượt tại E, F, P.
Gọi R = IP ∩ SA. Kéo dài PI cắt SO’ tại N
Gọi L = NF ∩ SC
Ta có thiết diện là ngũ giác IREFL.
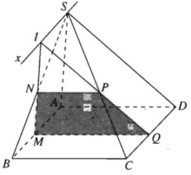
a) Vì M ∈ (SAB)
Và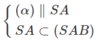 
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và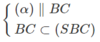 
nên (α) ∩ (SBC) = NP
và NP // BC (1)
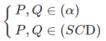⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và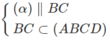 
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
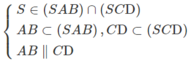⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒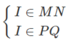 
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.
Tham khảo:
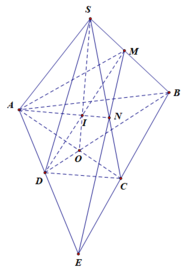
Ta có: DN thuộc (SBD) và MC thuộc (SAC)
Mà MC cắt DN tại I nên I là giao điểm của (SBD) và (SAC)
Ta có: S và O cùng thuộc hai mặt phẳng (SBD) và (SAC)
Theo tính chất 5: Các điểm S, O, I, đều thuộc giao điểm của hai mặt phẳng (SBD) và (SAC)
Vậy ba điểm S, O, I thẳng hàng.