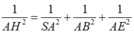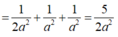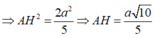Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Ta có AB// (SCD)
Kẻ O M ⊥ C D tại M, O K ⊥ S M tại K dễ có được O K ⊥ ( S C D )
Ta có:
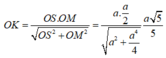
Vậy, d ( A B ; S C ) = 2 a 5 5
Chọn D
Phương pháp:
Sử dụng lý thuyết d(a,b) = d(a,(P)) = d (M,(P)) với a, b là các đường thẳng chéo nhau, (P) là mặt phẳng chứa chứa b và song song với a, M là một điểm bất kì thuộc a.
Cách giải:
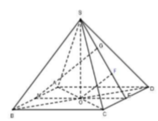
Gọi M, E là trung điểm của AB, CD và F, G là hinh chiếu của O, M lên SE.
Ta thấy:
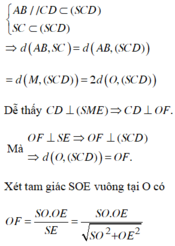
nhân 2 rồi chọn ngay C là sai.
Phương pháp:
- Dựng mặt phẳng chứa SO và song song với AB .
- Sử dụng lý thuyết: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường thẳng này đến mặt phẳng song song với nó và chứa đường thẳng kia.
- Đưa bài toán về tính khoảng cách từ điểm đến mặt phẳng và kết luận.
Cách giải:
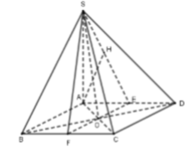
Gọi E, F lần lượt là trung điểm của AD, BC thì AB / / EF => AB / / (SEF)
Mà 
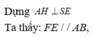
ABCD là hình vuông cạnh a nên BD = a 2
Dễ dàng chứng minh được 
Tam giác SBD cân có
S
B
D
=
60
0
Tam giác SAD vuông tại A có 
Tam giác SAE vuông tại A có
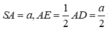
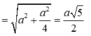
Do đó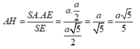 
Chọn D.
Chọn đáp án A
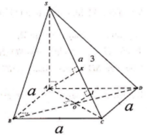
Gọi 
Ta có: 
Mặt khác 
=> OI là đường vuông góc chung.
=> d(BD;SC) = OI
Kẻ 
OI là đường trung bình của tam giác AKC.
Ta có: 
Xét tam giác SAC vuông tại A: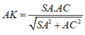 
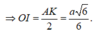
Vậy khoảng cách giữa BD và SC bằng a 6 6
Chọn A.
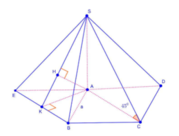
Góc giữa SC và mặt đáy bằng 45 o ⇒ S C A ^ = 45 o
Xét tam giác SAC vuông tại A, ta có
Dựng hình bình hành ACBE
Gọi H là hình chiếu của A lên mặt phẳng (SBE).
Xét hình tứ diện vuông SABE có
