Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
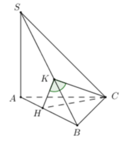
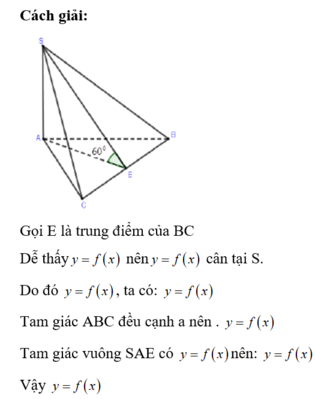
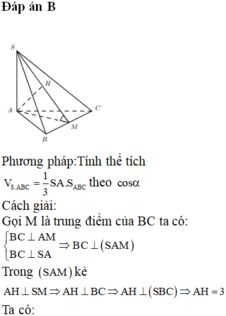
Gọi M là trung điểm của BC, ∆ S B C đều ⇒ S M ⊥ B C
Mà S A ⊥ ( A B C ) ⇒ S A ⊥ B C và S M ⊥ B C suy ra B C ⊥ ( S A M )
Ta có:
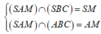
![]()
Xét tam giác SAM vuông tại A có:
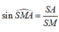
![]()
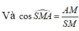
![]()
⇒ S A B C = 1 2 A M . B C = 3 a 2 8
⇒ V S . A B C = 1 3 S A . S A B C = a 3 3 32

1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.

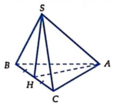
Đáp án D
Gọi M là trung điểm của BC, H là chân đường vuông góc kẻ từ A đến SM. Khi đó khoảng cách từ A đến mặt phẳng (SBC) bằng AH. Ta có:

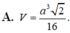
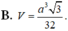
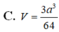
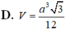
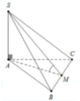
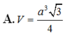
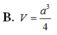
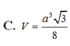
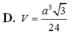


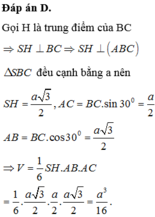
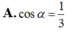

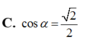
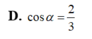
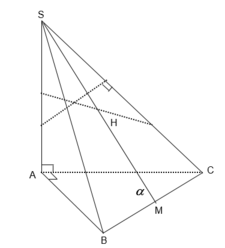

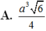
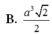
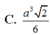
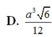

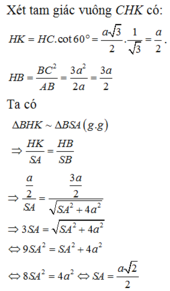
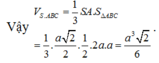
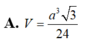
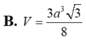
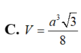
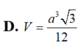


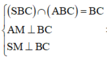
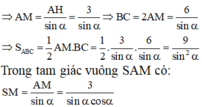
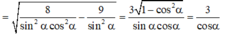
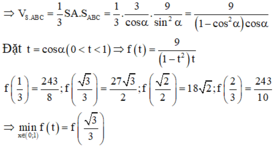
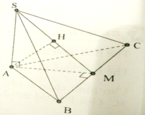
Đáp án B