Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
Cách giải: Gọi H là trung điểm của AC
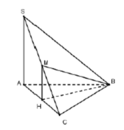
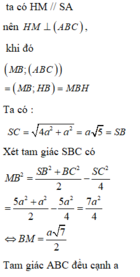
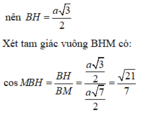

Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

Đáp án C
Gọi O là trung điểm của BC, suy ra O là tâm đường tròn ngoại tiếp tam giác ABC.
Ngoài ra, theo giả thiết ta có SA = SB = SC nên SO là trục của đường tròn ngoại tiếp tam giác ABC.
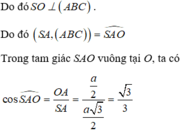
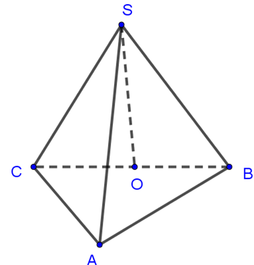

Đáp án là C.
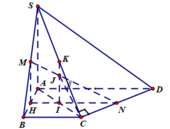

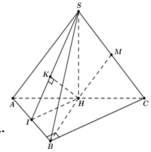
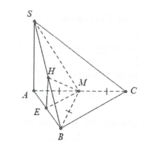
Ta dễ chứng minh được tam giácACD vuông tại C, từ đó chứng minh được CN vuông góc với mặt phẳng (SAC) hay C là hình chiếu vuông góc của N trên (SAC). Đường thẳng MN cắt mặt phẳng (SAC) tại J xác định như hình vẽ. Suy ra góc giữa MN và (SAC) là góc NJC .
IN là đương trung bình trong tam giác ACD suy ra IN=a, IH là đường trung bình trong tam giác ABC suy ra I H = 1 2 B C = a 2 . Dựa vào định lí Talet trong tam giác MHN ta được I J = 2 3 M H = 2 3 . 1 2 S A = 1 3 S A = a 3 . Dựa vào tam giác JIC vuông tại I tính được J C = 22 6 .
Ta dễ tính được C N = a 2 2 , J N = a 10 3 .
Tam giác NJC vuông tại C nên cos N J C ^ = J C J N = 55 10 .
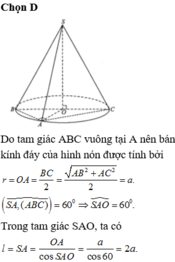

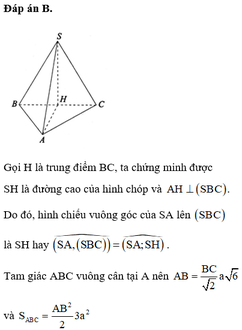
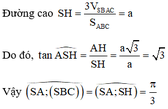

Đáp án B
Dựng hình bình hành AKCI khi đó S C ; A I ⏜ = S C ; C K ⏜
Ta có: A B = C K = A B 2 + B C 2 2 = a 6 2
S K = S A 2 + A K 2 = S A 2 + C I 2 = a 6 2
Khi đó cos S C K ⏜ = S C 2 + C K 2 − S K 2 2 S C . C K = 2 3 > 0 Do đó c os S C ; A I ⏜ = 2 3