Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
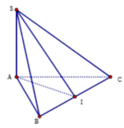
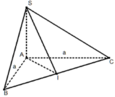
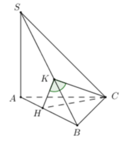
Gọi I là trung điểm của BC, tam giác ABC vuông cân tại A nên AI ⊥ BC
Có SA ⊥ (ABC) => SA ⊥ BC
Suy ra BC ⊥ (SAI). Suy ra ((SBC);(ABC)) = SIA.
∆ SIA vuông tại A có SA = a, AI = a. Suy ra vuông cân tại A.
Suy ra SIA = 45 °

Phương pháp:
Xác định góc giữa các mặt phẳng (P) và (Q) ta thực hiện các bước sau:
+ Xác định giao tuyến d của (P) và (Q)
+ Trong mặt phẳng (P) xác định đường thẳng a ⊥ d trong mặt phẳng (Q) xác định đường thẳng b ⊥ d
+ Khi đó góc giữa (P) và (Q) là góc giữa hai đường thẳng a và b
Cách giải:
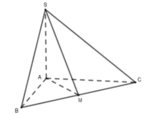
Gọi M là trung điểm BC => AM ⊥ BC (do ∆ ABC cân tại A).
Lại có ∆ SAB = ∆ SAC(c.g.c) hay ∆ SBC cân tại S
=> SM ⊥ BC
![]()
![]()

Theo đề bài
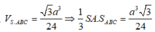
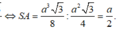
Lại thấy
∆
ABM vuông tại M có AB = a; ![]()
![]()
Xét tam giác SAM vuông tại A có SA = AM = a 2 nên ∆ SAM vuông cân tại A hay ∠ S M A = 45 °
Vậy góc giữa (SBC) và (ABC) bằng 45 °
Chọn D.

Ta có : \(SA\perp BC\), \(AB\perp BC\) \(\Rightarrow SB\perp BC\)
Do đó : góc giữa 2 mặt phẳng (SBC) và (ABC) bằng \(\widehat{SBA}=30^0\)
\(V_{S.ABM}=\frac{1}{2}V_{S.ABC}=\frac{1}{2}SA.AB.BC\)
\(BC=AB=a;SA=AB.\tan30^0=\frac{a\sqrt{3}}{3}\)
Vậy \(V_{s.ABM}=\frac{a^3\sqrt{3}}{36}\)


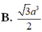
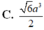
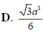
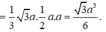
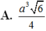
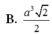
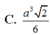
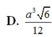

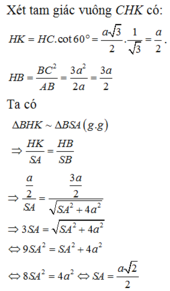
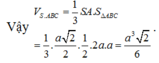
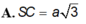
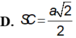



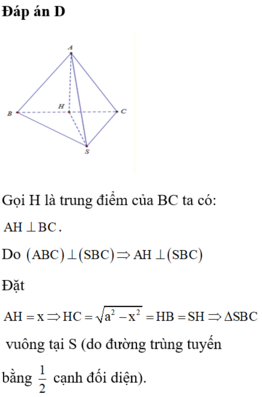

Chọn đáp án B
Gọi M là trung điểm BC.
Ta có: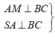
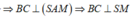
Suy ra góc giữa (SBC) và (ABC) bằng góc S M A ^
Tam giác ABC vuông cân tại A:
Xét tam giác SAM vuông tại A có SA = AM = a
=>Tam giác SAM vuông cân tại A => S M A ^ = 45 °