Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

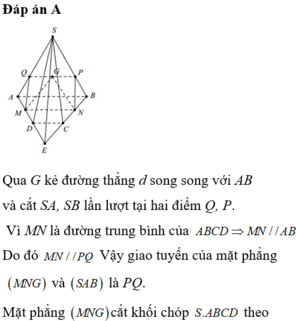
Do IJ là đường thẳng trung bình của hình thang ABCD nên IJ // AB. Hai mặt phẳng (GIJ) và (SAB) lần lượt chứa hai đường thẳng song song nên giao tuyến của chúng là đường thẳng đi qua G và song song với AB. Đường thẳng này cắt SA tại điểm M và cắt SB tại N. vậy thiết diện là hình thang MIJN, với M, N là giao điểm của đường thẳng đi qua G và song song với AB với hai đường thẳng SA, SB.
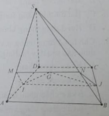
Đáp án B.

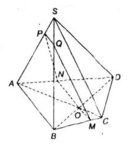
+ Ta có: (α) // AB
⇒ giao tuyến (α) và (ABCD) là đường thẳng qua O và song song với AB.
Qua O kẻ MN // AB (M ∈ BC, N ∈ AD)
⇒ (α) ∩ (ABCD) = MN.
+ (α) // SC
⇒ giao tuyến của (α) và (SBC) là đường thẳng qua M và song song với SC.
Kẻ MQ // SC (Q ∈ SB).
+ (α) // AB
⇒ giao tuyến của (α) và (SAB) là đường thẳng qua Q và song song với AB.
Từ Q kẻ QP // AB (P ∈ SA).
⇒ (α) ∩ (SAD) = PN.
Vậy thiết diện của hình chóp cắt bởi (α) là tứ giác MNPQ.
Ta có: PQ// AB và NM // AB
=> PQ // NM
Do đó, tứ giác MNPQ là hình thang.

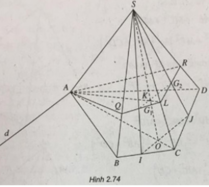
Gọi I, J lần lượt là trung điểm của BC, CD.
Ta có I J / / G 1 G 2 nên giao tuyến của hai mặt phẳng ( A G 1 G 2 ) và (ABCD) là đường thẳng d qua A và song song với IJ
Gọi O = IJ ∩ AC, K = G 1 G 2 ∩ S O , L = AK ∩ SC
L G 2 cắt SD tại R
L G 2 cắt SB tại Q
Ta có thiết diện là tứ giác AQLR.

Đáp án D
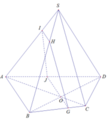
Trong mặt phẳng (ABCD), kẻ đường thẳng d đi qua O và song song với AB
d cắt AD tại J
d cắt BC tại G
Trong mặt phẳng (SBC), kẻ đường thẳng Gx đi qua G và song song với SC; đường thẳng này cắt SB tại H
Trong mặt phẳng (SAB), kẻ đường thẳng y đi qua H và song song với AB
y cắt SA tại I
⇒ IHGJ là thiết diện cần tìm
Xét tứ giác IHGJ có: IH // JG ( // AB )
⇒ IHGJ là hình thang

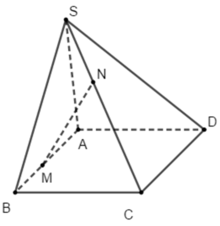
Kéo dài AD và BC cắt nhau tại E
\(\Rightarrow SE=\left(SAD\right)\cap\left(SBC\right)\)
Trong mp (SBC), nối MN kéo dài cắt SE tại F
Trong mp (SAD), nối AF cắt SD tại I
\(\Rightarrow I=SD\cap\left(AMN\right)\)
Tứ giác AINM chính là thiết diện của (AMN) và chóp
MN là đường trung bình tam giác SCD \(\Rightarrow F\) là trung điểm SE
Mặt khác CD song song và bằng 1/2 AB \(\Rightarrow\) CD là đường trung bình tam giác ABE hay D là trung điểm AE
\(\Rightarrow\) I là trọng tâm tam giác SAE
\(\Rightarrow\dfrac{SI}{SD}=\dfrac{2}{3}\)


Đáp án B
Trong mặt phẳng (ABCD) gọi I là giao điểm của MD và BC
Trong mặt phẳng (SBC) gọi K là giao điểm của IN và SB
Khi đó ta có: (MND) ∩ (SAB) = KM
(MND) ∩ (ABCD) = MD
(MND) ∩ (SBC) = KN
(MND) ∩ (SCD) = ND
Vậy thiết diện của mặt phẳng (MND) với hình chóp là tứ giác NDMK.
Đáp án B