Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

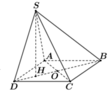
Xác định được ![]()
Tính được ![]()
![]()
Suy ra tam giác SBD vuông tại S. Vậy các đỉnh S, A, C cùng nhìn xuống BD dưới một góc vuông nên ![]()
Chọn B.

Chọn C.
Phương pháp:
Xác định trục của khối chóp sau đó dựng đường thẳng trung trực của một cạnh bên của khối chóp để tìm được tâm của mặt cầu.
Cách giải
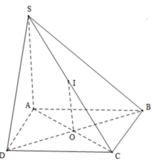
Gọi I là trung điểm của đoạn thẳng SC.
O là tâm của hình chữ nhật ABCD.
Ta chứng minh I là tâm mặt cầu ngoại tiếp hình chóp S.ABCD:
Do OI là đường trung bình của tam giác SAC => OI // SA


Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp chóp là giao điểm của trục của mặt đáy và mặt phẳng trung trực của 1 cạnh bên.
+) Áp dụng các kiến thức đã học tính bán kính mặt cầu. Từ đó áp dụng công thức tính diện tích mặt cầu bán kính R: S = 4 π R 2
Cách giải:
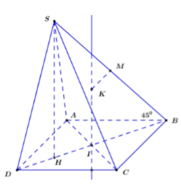
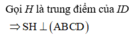
Qua I dựng đường thẳng d song song với SH, đường thẳng này chính là trục của hình chóp SABCD.
Dựng đường thẳng trung trực của cạnh SB,
cắt đường thẳng d tại K.
Khi đó K là tâm mặt cầu ngoại tiếp hình chóp S.ABCD



Đáp án C
Ta có A D 2 = A B 2 + B D 2 = A C 2 + C D 2
⇒ Δ A B D , Δ A C D vuông cân tại B, C
Mà O là trung điểm cạnh A D ⇒ O A = O B − O C
⇒ O là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Dễ thấy O A = O B − O C và Δ A B C đều cạnh a
⇒ khối chóp O . A B C là hình chóp tam giác đều

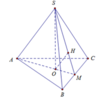
Đáp án A
Ta có O M = 1 3 A M = a 3 3
Lại có d O ; S B C = O H = a 2 ⇒ S O = a
Mặt khác R N = O A = 2 a 3 3 ; h = S O = a ⇒ V = 1 3 π R 2 h = 4 π a 3 9



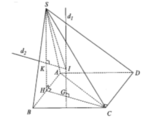


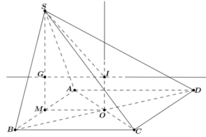


Đáp án B
Vì A C = B D = a 2 ⇒ Δ S A C ; Δ S B D vuông tại S