Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì SABC là hình chóp đều nên nó sẽ có tính đối xừng, và cách làm giống bài bên trên toi vừa làm, bạn tham khảo

Gọi M là trung điểm AB là N là trung điểm BM
\(\Rightarrow CM\perp AB\) (trung tuyến đồng thời là đường cao trong tam giác đều)
NH là đường trung bình tam giác BCM \(\Rightarrow NH||CM\Rightarrow NH\perp AB\)
\(\Rightarrow AB\perp\left(SNH\right)\) \(\Rightarrow\left(SAB\right)\perp\left(SNH\right)\) với SN là giao tuyến
Trong mp (SNH), từ H kẻ \(HK\perp SN\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
\(CM=\dfrac{AC\sqrt{3}}{2}=6a\) ; \(NH=\dfrac{1}{2}CM=3a\)
\(\widehat{SNH}=60^0\Rightarrow HK=NH.sin60^0=\dfrac{3a\sqrt{3}}{2}\)

Gọi H là trung điểm AB \(\Rightarrow SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp BC\)
Mà \(BC\perp AB\Rightarrow BC\perp\left(SAB\right)\)
Gọi K là trung điểm CD \(\Rightarrow HK||BC\Rightarrow HK\perp AB\Rightarrow HK\perp\left(SAB\right)\)
Trong tam giác SHK, kẻ \(HI\perp SK\Rightarrow HI\perp\left(SCD\right)\)
\(\Rightarrow HI=d\left(H;\left(SCD\right)\right)\)
Mà \(AH||CD\Rightarrow AH||\left(SCD\right)\Rightarrow d\left(A;\left(SCD\right)\right)=d\left(H;\left(SCD\right)\right)=HI\)
\(SH=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) ; \(HK=BC=a\)
\(\dfrac{1}{HI^2}=\dfrac{1}{SH^2}+\dfrac{1}{HK^2}=\dfrac{7}{3a^2}\Rightarrow HI=\dfrac{a\sqrt{21}}{7}\)
b. Theo cmt ta có \(BC\perp\left(SAB\right)\Rightarrow d\left(C;\left(SAB\right)\right)=BC=a\)
c. \(BC||AD\Rightarrow d\left(C;\left(SAD\right)\right)=d\left(B;\left(SAD\right)\right)\)
Mà BH cắt (SAD) tại A, đồng thời \(BA=2HA\Rightarrow d\left(B;\left(SAD\right)\right)=2d\left(H;\left(SAD\right)\right)\)
Từ H kẻ \(HM\perp SA\Rightarrow HM\perp\left(SAD\right)\Rightarrow HM=d\left(H;\left(SAD\right)\right)\)
\(\dfrac{1}{HM^2}=\dfrac{1}{SH^2}+\dfrac{1}{AH^2}=\dfrac{16}{3a^2}\Rightarrow HM=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow d\left(C;\left(SAD\right)\right)=2HM=\dfrac{a\sqrt{3}}{2}\)

Chọn đáp án B
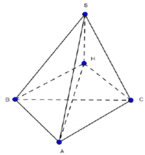
Gọi là H hình chiếu của đỉnh S xuống mặt phẳng (ABC). Khi đó, ta có
![]()
Ta có
![]()
Tương tự, ta cũng chứng minh được
![]()
Từ đó suy ra
![]()
Do SH ⊥ AB, BH ⊥ AB nên suy ra góc giữa (SAB) và (ABC) là góc SBH. Vậy SBH = 60 0
![]()
Trong tam giác vuông ABH, ta có
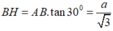
Trong tam giác vuông SHB, ta có
![]()
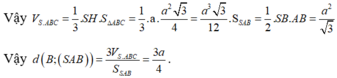


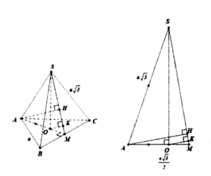

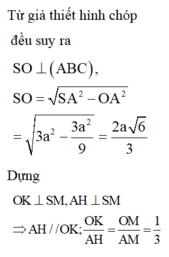


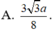
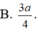
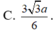
Cho mik hỏi H ở đâu đấy