Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

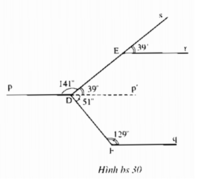
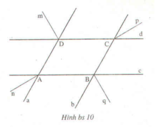
+) Ta có hai đường thẳng DE và DF cắt nhau tại D.
+) Kẻ tia Dp’ là tia đối của tia Dp.
+) Do Er // Dp nên Er // Dp’
Suy ra

+) Ta có tia Dp’ nằm giữa hai tia DF và tia DE nên:

Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.

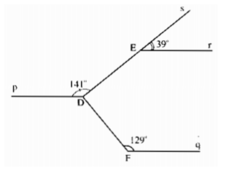
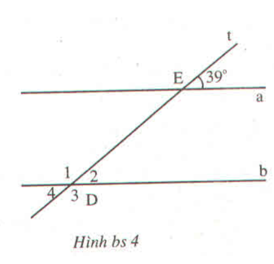
∠D2 = 39° vì là góc đồng vị với ∠E = 39°.
∠D4 = 39° vì là góc đối đỉnh với ∠D2.
∠D3 = 141° vì bù với góc ∠D4.
∠D1 = 141° vì là góc đối đỉnh với ∠D3.

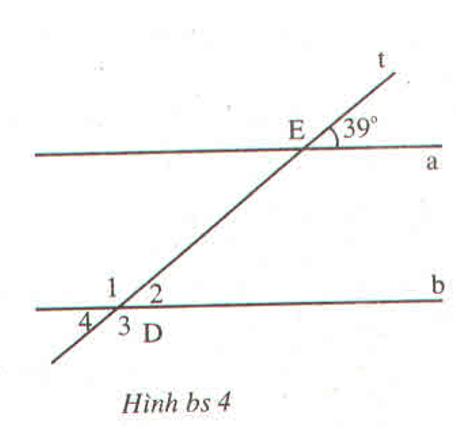
∠D2 = 39° vì là góc đồng vị với ∠E
∠D4 = 39° vì là góc đối đỉnh với ∠D2
∠D3 = 141° vì bù với góc ∠D4
∠D1 = 141° vì là góc đối đỉnh với ∠D3

a) p có song song với q
b) m vuông góc với q
c) Hai đường thẳng p và q vuông góc với nhau
d) Hai đường thẳng p và q vuông góc với nhau

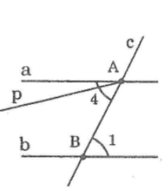
Một cặp góc so le trong là cặp góc A4 và B1. Ta đo thấy chúng có số đo bằng nhau:
∠(A4) = ∠(B1)

b
(B) \(^{135^0}\)