Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔADNΔADN và ΔMBAΔMBA có:
ˆDAN=ˆBMADAN^=BMA^ (AB//DC nên hai góc ở vị trí so le trong bằng nhau)
ˆAND=ˆMABAND^=MAB^ (hai góc ở vị trí so le trong)
⇒ΔADN∼ΔMBA⇒ΔADN∼ΔMBA (g.g)
⇒DNBA=DABM⇒DNBA=DABM (hai cạnh tương ứng)
⇒BM.DN=BA.DA⇒BM.DN=BA.DA mà BA,DABA,DA là hai cạnh của hình bình hành, hình bình hành cố định nên BM.DNBM.DN cố định (đpcm)
mình nghĩ dc câu a thôi

Mk ms nghĩ được phần a thôi, phần b để tí nghĩ tiếp :v
(Hình tự vẽ)
Vì ABCD là hình bình hành (gt)
\(\Rightarrow\) AD//BC (t/c hbh)
Mà M \(\in\) BC (d cắt BC tại M)
\(\Rightarrow\) AD//MB
\(\Rightarrow\) \(\widehat{DAN}=\widehat{AMB}\) (2 góc slt, N \(\in\) AM)
Vì ABCD là hbh (gt)
\(\Rightarrow\) \(\widehat{B}=\widehat{D}\) (t/c hbh)
Xét tam giác ADN và tam giác MBA có:
\(\widehat{D}=\widehat{B}\) (cmt)
\(\widehat{DAN}=\widehat{BMA}\) (cmt)
\(\Rightarrow\) \(\Delta\)ADN \(\sim\) \(\Delta\)MBA (gg)
\(\Rightarrow\) \(\dfrac{AD}{BM}=\dfrac{DN}{AB}\) (tỉ số đồng dạng)
\(\Rightarrow\) BM.DN = AB.AD
Mà AB, AD là các cạnh của hbh (gt)
\(\Rightarrow\) AB, AD không đổi
\(\Rightarrow\) AB.AD không đổi
\(\Rightarrow\) MB.DN không đổi (đpcm)
Chúc bn học tốt!

 a) *) Chứng minh AMNB là hình bình hành:
a) *) Chứng minh AMNB là hình bình hành:
Do O là giao điểm của AC và BD
Mà ABCD là hình bình hành (gt)
⇒ O là trung điểm của AC và BD
Do MN // AB (gt)
⇒ OM // CD
∆ACD có
O là trung điểm AC
OM // CD
⇒ M là trung điểm AD
⇒ AM = AD : 2 (1)
Do MN // AB (gt)
⇒ ON // AB
∆ABC có:
O là trung điểm AC (cmt)
ON // AB (cmt)
⇒ N là trung điểm BC
⇒ BN = BC : 2 (2)
Do ABCD là hình bình hành (gt)
⇒ AD // BC
⇒ AM // BN
Từ (1) và (2) ⇒ AM = BN
Tứ giác AMNB có:
AM // BN (cmt)
AM = BN (cmt)
⇒ AMNB là hình bình hành
*) Chứng minh APCQ là hình bình hành
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AP // CQ
Tứ giác APCQ có:
AP // CQ (cmt)
AP = CQ (gt)
⇒ APCQ là hình bình hành
c) Do O là trung điểm AC (cmt)
M là trung điểm AD (cmt)
⇒ OM là đường trung bình của ∆ACD
⇒ OM = CD : 2 (3)
Do O là trung điểm AC (cmt)
N là trung điểm BC (cmt)
⇒ ON là đường trung bình của ∆ABC
⇒ ON = AB : 2
Mà AB = CD (do ABCD là hình bình hành)
⇒ OM = ON
⇒ O là trung điểm MN
Do APCQ là hình bình hành (cmt)
O là trung điểm AC (cmt)
⇒ O là trung điểm PQ
Tứ giác MPNQ có:
O là trung điểm MN (cmt)
O là trung điểm PQ (cmt)
⇒ MPNQ là hình bình hành
⇒ MP // NQ và MQ = NP

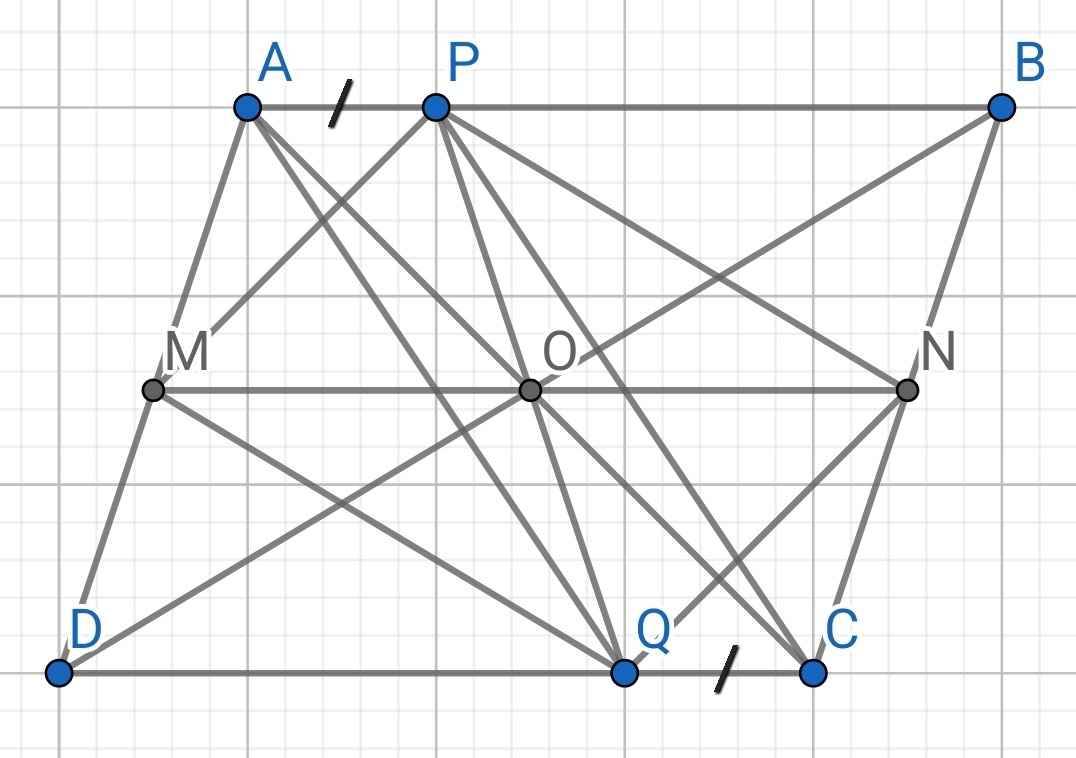
A B C D O M N P Q
a/
Ta có
MN//AB (gt)
AD//BC=> AM//BN
=> AMNB là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có
AB//CD => AP//CQ mà AP = CQ (gt) => APCQ là hbh (Tứ giác có cặp cạnh đối // và = nhau là hbh)
b/
Xét hbh ABCD
OA=OC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Xét hbh APCQ có
IA=IC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> \(I\equiv O\) (đều là trung điểm AC) => M; N; I thẳng hàng
c/ Do \(I\equiv O\) (cmt) => AC; MN; PQ đồng quy tại O