Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc AED+góc AEC=180 độ
góc AEC+góc ABC=180 độ
Do đó: góc AED=góc ABC
=>góc AED=góc ADE
=>AD=AE

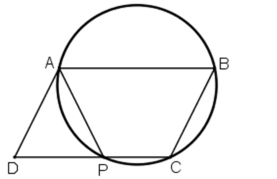
Đường tròn đi qua 3 đỉnh A,B,C cắt đường thẳng CD tại P (gt)
=>ABCP là tứ giác nội tiếp
=>Góc APC+góc ABC =180 (1)
ABCD là hình bình hành (gt)
=>góc ADC = góc ABC hay góc ADP=góc ABC (vì D,P,C thẳng hàng theo gt) (2)
Từ (1) và (2) => góc APC + góc ADP=180 (3)
Mà góc APD+góc APC =180 (kề bù) (4)
Từ (3) và (4) =>góc APD=góc ADP
=> tam giác ADP cân tại A
=> AP=AD (đpcm)
+ Do ABCD là hình bình hành nên AB // CD
\(\Rightarrow\widehat{ABC}+\widehat{BCP}=180^o\) ( hai góc trong cùng phía ) (1)
+ ABPC là tứ giác nội tiếp
\(\Rightarrow\widehat{PAB}+\widehat{BCP}=180^o\)(2)
Từ (1) và (2) , suy ra : \(\widehat{PAB}=\widehat{ABC}\)
+ Tứ giác ABPC có : AB // CP ( Vì AB // CD )
=> Tứ giác ABCP là hình thang
Ta lại có : \(\widehat{PAB}=\widehat{ABC}\)nên ABCP là hình thang cân
=> AP = BC (3)
Mà ABCD là hình bình hành => AD = BC (4)
Từ (3) và (4)) , suy ra : \(AP=AD\left(đpcm\right)\)

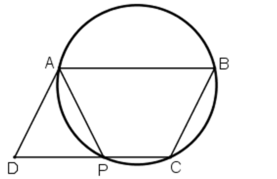
+ Do ABCD là hình bình hành nên AB//CD
⇒ A B C ^ + B C P ^ = 180 o (hai góc trong cùng phía) (1)
+ ABCP là tứ giác nội tiếp
⇒ P A B ^ + B C P ^ = 180 o 2
Từ (1) và (2) suy ra: P A B ^ = A B C ^
+ Tứ giác ABCP có: AB//CP (vì AB//CD)
=> Tứ giác ABCP là hình thang.
Lại có: P A B ^ = A B C ^ nên ABCP là hình thang cân.
=> AP=BC (3)
Mà ABCD là hình bình hành => AD = BC (4)
Từ (3) và (4) suy ra AP=AD (đpcm).

a: Ta có: AD//BC
AC\(\perp\)AD
Do đó: AC\(\perp\)BC
Xét ΔBAK vuông tại A có AC là đường cao ứng với cạnh huyền BK, ta được:
\(CB\cdot CK=AC^2\left(1\right)\)
Xét ΔADC vuông tại A có AH là đường cao ứng với cạnh huyền CD,ta được:
\(CH\cdot CD=AC^2\left(2\right)\)
Từ (1) và(2) suy ra \(CB\cdot CK=CH\cdot CD\)

Do tứ giác ABCP nội tiếp nên ta có:
+
= 180o (1)
Ta lại có: +
= 180o (2)
(hai góc trong cùng phía tạo bởi cát tuyến CB và AB // CD)
Từ (1) và (2) suy ra: =
Vậy ABCP là hình thang cân, suy ra AP = BC (3)
nhưng BC = AD (hai cạnh đối đỉnh của hình bình hành) (4)
Từ (3) và (4) suy ra AP = AD.
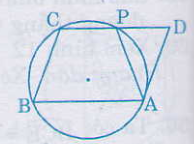
Do tứ giác ABCP nội tiếp nên ta có:
+
= 180o (1)
Ta lại có: +
= 180o (2)
(hai góc trong cùng phía tạo bởi cát tuyến CB và AB // CD)
Từ (1) và (2) suy ra: =
Vậy ABCP là hình thang cân, suy ra AP = BC (3)
nhưng BC = AD (hai cạnh đối đỉnh của hình bình hành) (4)
Từ (3) và (4) suy ra AP = AD.