Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình
=>EF//AC và EF=AC/2(1)
Xét ΔCDA có
G là trung điểm của CD
H là trung điểm của DA
Do đó: GH là đường trung bình
=>GH//AC và GH=AC/2(2)
Từ (1) và (2) suy ra EF//GH và EF=GH
hay EFGH là hình bình hành
b: EF=GH=AC/2=3(cm)
FG=EH=BD/2=4(cm)

a) nối A với C , B với D được:
EF // AC ( đường trung bình của tam giác BAC)
HG // AC ( " " " " " " ) suy ra EF // AC do cùng // AC
HE // DB ( đường trung bình tam giác ADB )
FG // DB ( " " " " " " ) suy ra HE // FG do cùng // với DB
Xét tứ giác EFGH có 2 cặp cạnh đối song song nên EFGH là hình bình hành
b) EFGH là hình ....
Thoi , suy ra EH = GH nên AC=BD ( do là đường trung bình của hai tam giác ADB,ADC)
vì AC = BD nên ABCD là hình thang cân
Chữ nhật, suy ra HE vuông góc với HG nên AC vuông góc với BD
Hình vuông , kết hợp 2 yếu tố của 2 hình trên được AC=BD và AC vuông góc với BD.
Tích nha☺

a) Mình đề nghị bạn giở SGK toán 8 tập 1 trang 93 bài 7 hình học chương I nhé.
b) Ta có: \(AC\perp BD\)
mà HE//BD=>\(HE\perp AC\)
mà AC//HG
=> \(\widehat{EHG}=90^o\)
Chứng minh tương tự với 2 trong 3 góc còn lại của tứ giác EFGH.
=> Nếu AC vuông góc với BD thì EFHG là hình chữ nhật.
Đây là hướng làm nhé, còn bạn hiếu sao thì trình bày theo ý bạn nhé:vv

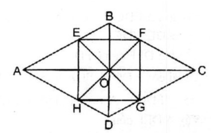
Ta có: ∠ (AOB) và ∠ (COD) đối đỉnh nên E, O, G thẳng hàng
∠ (BOC) và ∠ (AOD) đối đỉnh nên F, O, H thẳng hàng
Xét ∆ BEO và ∆ BFO:
∠ (EBO) = ∠ (FBO) (tính chất hình thoi)
OB cạnh chung
∠ (EOB) = ∠ (FOB) = 45 0 (gt)
Do đó: ∆ BEO = ∆ BFO (g.c.g)
⇒ OE = OF (1)
Xét ∆ BEO và ∆ DGO:
∠ (EBO) = ∠ (GDO) (so le trong)
OB = OD(tính chất hình thoi)
∠ (EOB) = ∠ (GOD) (đối đỉnh)
Do đó: ∆ BEO = ∆ DGO (g.c.g)
⇒ OE = OG (2)
Xét ∆ AEO và ∆ AHO:
∠ (EAO) = ∠ (HAO) (tính chất hình thoi)
OA cạnh chung
∠ (EOA) = ∠ (HOA) = 45 0 (gt)
Do đó: ∆ AEO = ∆ AHO (g.c.g)
⇒ OE = OH (3)
Từ (1), (2) và (3) suy ra: OE = OF = OG = OH hay EG = FH
nên tứ giác EFGH là hình chữ nhật (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và bằng nhau)
OE ⊥ OF (tính chất tia phân giác của hai góc kề bù)
hay EG ⊥ FH
Vậy hình chữ nhật EFGH là hình vuông.

Xét ΔABD có
E,H lần lượt là trung điểm của AB,AD
=>EH là đường trung bình
=>EH//BD và EH=BD/2
Xét ΔBCD có
G,F lần lượt là trung điểm của CD,CB
=>GF là đường trung bình
=>GF//BD và GF=BD/2
=>EH//GF và EH=GF
=>EFGH là hình bình hành