Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
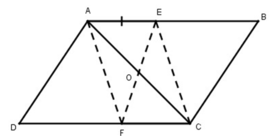
Gọi O là giao điểm của hai đường chéo AC và BD.
Xét tứ giác AECF:
AB // CD (gt)
⇒ AE // CF
AE = CF (gt)
Suy ra: Tứ giác AECF là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
⇒ AC và EF cắt nhau tại trung điểm mỗi đường
OA = OC ( tính chất hình bình hành) ⇒ EF đi qua O
Vậy AC, BD, EF đồng quy tại O.
Hình bình hành ABCD có :
AC cắt BD tại trung điểm của AC và BD ( 1 )
Hình bình hành EBFD có :
EF cắt BD tại trung điểm của EF và BD ( 2 )
\(\Rightarrow\)Từ ( 1 ) và ( 2 ) suy ra AC ; BD ; EF đồng quy
a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Gọi O là giao điểm 2 đường chéo AC và BD
Xét \(\Delta\)AOE và \(\Delta\)COF có:AO=OC ( vì ABCD là hình bình hành ),CF=AE ( giả thiết ),^AOE=^COF ( đối đỉnh )
a
Vì vậy \(\Delta AOE=\Delta COF\left(c.g.c\right)\Rightarrow OE=OF\left(1\right)\)
Xét \(\Delta\)BON và \(\Delta\)DOM có:OB=OD ( vì ABCD là hình bình hành ),MD=BN ( vì AM=CN ),^MOD=^NOB ( đối đỉnh )
Vì vậy \(\Delta BON=\Delta COM\left(c.g.c\right)\Rightarrow OM=ON\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) suy ra tứ giác EMFN là hình bình hành.
b
Hình bình hành EMFN có O là giao điểm của 2 đường chéo,tứ giác ABCD có O là giao điểm của 2 đường chéo.
=> ĐPCM
P/S:Mik ko chắc lắm đâu nha,nhất là câu b ý:p
