Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F G H
Xét \(\Delta ADB\):
\(AE=EB\left(gt\right)\)
\(HD=HA\left(gt\right)\)
\(\Rightarrow HE\)là đường trung binh cũa \(\Delta ADB\).
\(\Rightarrow HE\)//\(DB\)và \(HE=\frac{1}{2}DB\left(1\right)\)
Xét \(\Delta CDB:\)
\(FB=FC\left(gt\right)\)
\(GC=GD\left(gt\right)\)
\(\Rightarrow GF\) là dường trung bình của \(\Delta CBD\).
\(\Rightarrow GF\)//\(DB\)và \(GF=\frac{1}{2}DB\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\)\(HE\)//\(GF\)và \(HE=GF\)
Vậy tứ giác \(EFGH\)là hình bình hành.
b) Xét \(\Delta AEH\)và \(\Delta EBF\):
\(AE=EB\left(gt\right)\)
Góc A = Góc B = 90o (ABCD là hình chữ nhật)
\(AD=BC\Rightarrow\frac{1}{2}AD=\frac{1}{2}BC\Rightarrow AH=BF\)
\(\Rightarrow\Delta AEH=\Delta EBF\left(c.g.c\right)\)
\(\Rightarrow HE=HF\)
mà tứ giác EFGH là hình bình hành.
Vậy hình bình hành \(EFGH\)là hình thoi.

Nối AC
a, Xét t/g ABC có: EA=EB(gt),FB=FC(gt)
=>EF là đường trung bình của t//g ABC
=>EF // AC (1), EF=1/2AC (2)
CMTT ta có: HG//AC (3), HG = 1/2AC (4)
Từ (1),(2),(3),(4) => EF//HG, EF=HG
=> EFGH là HBH
b, để HBH EFGH là hình thoi <=> EF = EH
=> t/g AHE = t/g BFE
=> góc EAH = góc EBF
=> hình thang ABCD cân

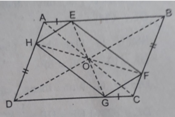
AE//CG, AE = CG nên AECG là hình bình hành ⇒ O là trung điểm của EG. Tương tự O là trung điểm của HF.

kẻ BD
ta có HA=HD
EA=EB
=> HE là đg tb cuả tam giác ABD
=> HE//BD; HE=1/2BD (1)
cmtt ta có GF là đg tb cuả tam giác CBD
=> GF//BD;GF=1/2BD (2)
Từ (1)và (2)
=>HE=GF(=1/2BD); HE//GF(//BD)
=> EFGH là hình bình hành
a: AE=EB=AB/2
CG=GD=CD/2
mà AB=CD
nên AE=EB=CG=GD
AH=HD=AD/2
BF=FC=BC/2
mà AD=BC
nên AH=HD=BF=FC
b: Xét ΔAHE và ΔCFG có
AH=CF
góc A=góc C
AE=CG
=>ΔAHE=ΔCFG
c: Xét ΔEBF và ΔGDH có
EB=GD
góc B=góc D
BF=DH
=>ΔEBF=ΔGDH
=>GH=EF
d: Xét tứ giác EHGF có
EH=FG
EF=GH
=>EHGF là hình bình hành