PD
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
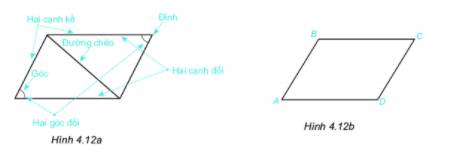
1) Ta đo được: AB = CD; BC = AD. Vậy các cạnh đối của hình bình hành bằng nhau
2) OA = OC; OB = OD
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình bình hành song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2021
Do \(DC=3EC\Rightarrow S_{ABCD}=3S_{FBCE}\)
\(\Rightarrow S_{FBCE}=\dfrac{48}{3}=16\left(m^2\right)\)
3 tháng 12 2021
Chiều cao là \(\dfrac{10+10}{2}=10\left(cm\right)\)
Diện tích hbh là \(10\cdot6=60\left(cm^2\right)\)
KV
4 tháng 11 2023
Chu vi hình bình hành ABCD:
(AB + AD) . 2 = 90 (cm)
AB + AD = 90 : 2 = 45 (cm)
\(2x+x=45\left(cm\right)\)
\(3x=45\left(cm\right)\)
\(x=45:3=15\left(cm\right)\)
\(\Rightarrow AB=2.15=30cm;AD=15cm\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
5 tháng 5 2022
Ta có CF=DE=CD=4 cm
=> BC=AD=32:2-4=12 cm
Hình thoi CDEF và hình bình hành ABCD có chung đường cao từ C->AE nên
\(\dfrac{S_{CDEF}}{S_{ABCD}}=\dfrac{DE}{AD}=\dfrac{4}{12}=\dfrac{1}{3}\Rightarrow S_{ABCD}=3.S_{CDEF}=3.54=162cm^2\)
Ta có:
\(\widehat{A}=\widehat{C}=50^o\)
\(\widehat{B}=\widehat{C}=130^o\)
nhanh lên