K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
4 tháng 2 2019
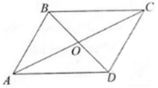
a) Ta có:
O là trung điểm của AC nên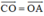 
Do đó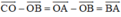 
b) ABCD là hình bình hành nên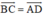 
Do đó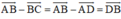 
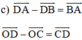
Mà ABCD là hình bình hành nên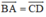 
Do đó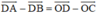 
d) ABCD là hình bình hành nên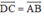 
Lại có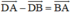 
Do đó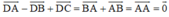 
PT
1
DP
1
10 tháng 2 2022
Xét tứ giác KHCD có
KH//CD
KH=CD
Do đó: KHCD là hình bình hành
Suy ra: \(\overrightarrow{CH}=\overrightarrow{DK}\)
PT
1
PT
1
CM
20 tháng 9 2017
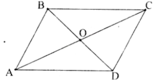
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
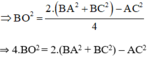
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Cách 1:
Do ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {AM} + \overrightarrow {MB} = \overrightarrow {DM} + \overrightarrow {MC} \\ \Leftrightarrow - \overrightarrow {MA} + \overrightarrow {MB} = - \overrightarrow {MD} + \overrightarrow {MC} \\ \Leftrightarrow \overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \end{array}\)
Cách 2:
Ta có: \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \Leftrightarrow \overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {MD} - \overrightarrow {MC} \) (*)
Áp dụng quy tắc hiệu ta có: \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {BA} ;\;\;\overrightarrow {MD} - \overrightarrow {MC} = \overrightarrow {CD} \)
Do đó (*) \( \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CD} \) (luôn đúng do ABCD là hình bình hành)
Cách 3:
Ta có:
\(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {BA} + \overrightarrow {MD} + \overrightarrow {DC} = \overrightarrow {MB} + \overrightarrow {MD} + \left( {\overrightarrow {BA} + \overrightarrow {DC} } \right)\)
Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \)\( \Rightarrow - \overrightarrow {BA} = \overrightarrow {DC} \) hay \(\overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \) (đpcm)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Tứ giác ABCD là hình bình hành
\( \Leftrightarrow \left\{ \begin{array}{l}
AB // DC\\
AB = DC
\end{array} \right.\)
Mà \(AB // DC \Leftrightarrow \overrightarrow {AB} ,\, \overrightarrow {DC} \) cùng phương, do đó cùng hướng.
\( \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} , \overrightarrow {DC} \,{\rm{ cùng hướng}}\\
AB = DC
\end{array} \right.\)
\(\Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \)
Vậy tứ giác ABCD là hình bình hành khi và chỉ khi \(\overrightarrow {AB} = \overrightarrow {DC} \).
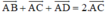
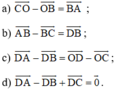
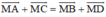
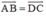
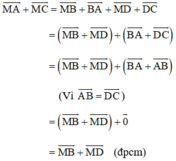
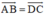
ABCD là hình bình hành