Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c.
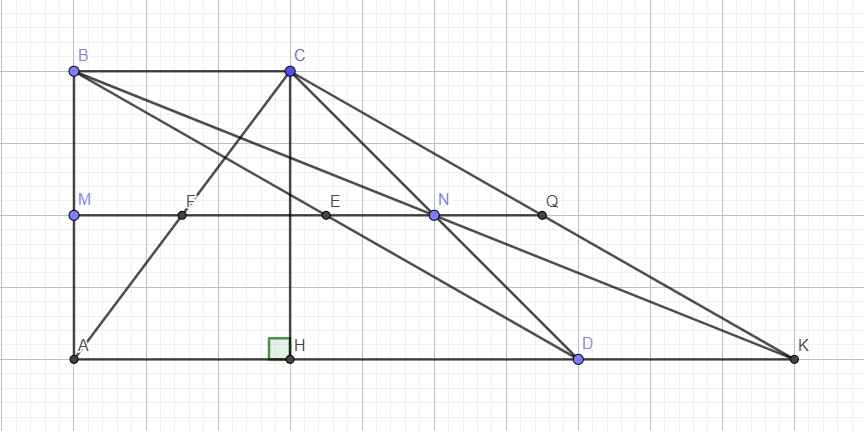
K thuộc AD nên BC song song DK
Áp dụng định lý Talet: \(\dfrac{BN}{KN}=\dfrac{CN}{DN}=1\Rightarrow BN=KN\) hay N là trung điểm BK
\(\Rightarrow\) BCKD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Theo câu b, E, M, N thẳng hàng nên Q nằm trên MN (1)
Mà MN là đường trung bình của hình thang ABCD
\(\Rightarrow MN||AD\Rightarrow MN\perp AB\) (2)
Mà M là trung điểm AB (3)
(2);(3) \(\Rightarrow\) MN là trung trực AB (4)
(1);(4) \(\Rightarrow QB=QA\)
d.
Hạ CH vuông góc AD
Trong tam giác vuông CHK: \(cosKAC=\dfrac{AH}{AC}\Rightarrow AH=AC.cos\widehat{KAC}\)
Pitago: \(CH^2+AH^2=AC^2\)
Do đó: \(CK^2=CH^2+HK^2=CH^2+\left(AK-AH\right)^2=CH^2+AH^2+AK^2-2AK.AH\)
\(=AC^2+AK^2-2AK.AC.cos\widehat{KAC}\) (đpcm)

Gọi M là trung điểm BC => BM=CM
Xét tam giác ABC có:
BM=CM
AE=EC (giả thiết vì E la trung điểm của AC)
Nên: EM là đường trung bình trong tam giác ABC
=>EM//AB và EM=AB/2
Tương tự: Xét tam giác BCD có:
FM là đường trung bình trong tam giác BCD
=>FM//CD và FM=CD/2
Lại có:
FM//CD
mà AB//CD (theo giả thiết ABCD la hthang)
Nên: FM//AB
Mà EM//AB
Do đó, theo tiên đề Ơclit ta có: E,M,F thẳng hàng.
Vậy,EF=FM-EM=(CD-AB)/2

1. Ta có:
ED,EAED,EA là tiếp tuyến của (O)
→ED⊥OD,EA⊥OA⇒ˆADE=ˆOAE=90o→ED⊥OD,EA⊥OA⇒ADE^=OAE^=90o
EDOAEDOA có ˆADE+ˆOAE=180oADE^+OAE^=180o
⇒EDOA⇒EDOA nội tiếp đường tròn đường kính (OE)
→ˆDOA+ˆDEA=180o→DOA^+DEA^=180o
Mà ABCDABCD là hình thang cân
→ˆDMA=ˆDBA+ˆCAB=2ˆDBA=ˆDOA→DMA^=DBA^+CAB^=2DBA^=DOA^
→ˆDMA+ˆAED=180o→AEDM→DMA^+AED^=180o→AEDM nội tiếp được trong một đường tròn
2. Từ câu 1
→ˆEMA=ˆEDA=ˆDBA=ˆCAB→EMA^=EDA^=DBA^=CAB^
Vì EDED là tiếp tuyến của (O),ABCDABCD là hình thang cân
→EM//AB→EM//AB
3. Ta có:
EM//AB→HK//AB→HMAB=DMDB=CMCA=MKABEM//AB→HK//AB→HMAB=DMDB=CMCA=MKAB
→MH=MK→M→MH=MK→M là trung điểm HK


gọi M là trung điểm của AF . Ta có OM là đường trung bình của tam giác ACF
\(=>OM//CF,OM=\frac{1}{2}CF\)
ta lại có \(OM//CF,CF\perp CD\left(gt\right)\)
\(=>OM\perp CD.Mà\left(AB//CD\right)\)
\(=>OM//BE\)(1)
mặt khác OM , AM là 2 đường cao của tam giác ABO
=> M là trực tâm của tam giác ABO
=>\(BM\perp AC.Mà\left(EO\perp AC\right)=>BM//EO\left(2\right)\)
từ 1 zà 2 => tứ giác BMOE là hbh => OM=BE
ta có
\(OM=BE;OM=\frac{1}{2}CF=>BE=\frac{1}{2}CF\left(and\right)BE//OM//CF\)
\(\Delta KCF\)có \(CF//BE=>\frac{KE}{KF}=\frac{BE}{CF}=\frac{1}{2}\)

Người quen nhờ vả à Hậu vừa hỏi mình bài này xong mình cũng bó tay