
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


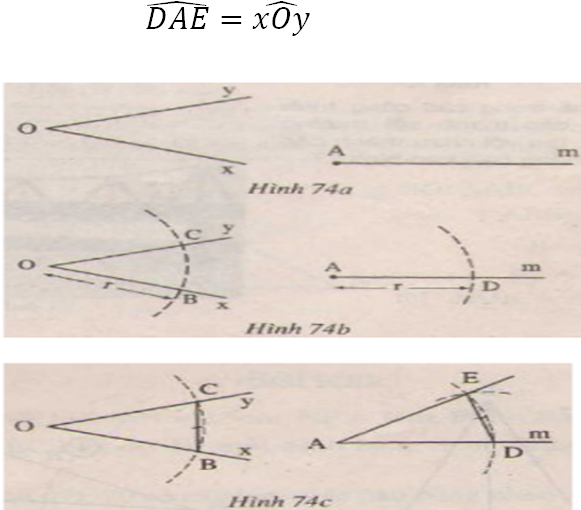
Hai tam giác ADE và OCB có:
OB = AD = r
BC = DE ( giả thiết )
OC = AE = r
\(\Rightarrow\Delta ADE=\Delta OBC\) (c.c.c)
Vậy \(\widehat{DAE}=\widehat{xOy}\) ( góc tương ứng) (đpcm)
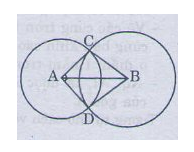
Hai tam giác ACB và ADB có:
AC = AD = 2 cm
BC = BD = 3 cm
AB cạnh chung
\(\Rightarrow\Delta ACB=\Delta ADB\) (c.c.c)
\(\Rightarrow\widehat{CAB}=\widehat{DAB}\) ( góc tương ứng )
Vậy AB là tia phân giác của góc CAD
bài 22
Tam giác DAE và BOC có:
AD=OB(gt)
DE=BC(gt)
AE=OC(gt)
Nên ∆ DAE= ∆ BOC(c.c.c)
suy ra ˆDAEDAE^=ˆBOCBOC^(hai góc tương tứng)
vậy
ˆDAE=ˆxOy.DAE^=xOy^.
bài 23
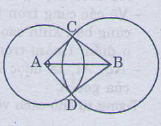
Vì CC là giao của đường tròn tâm AA và tâm BB nên AC=2cm,BC=3cmAC=2cm,BC=3cm
Vì DD là giao của đường tròn tâm AA và tâm BB nên AD=2cm,BD=3cmAD=2cm,BD=3cm
Do đó AC=AD,BC=BDAC=AD,BC=BD
Xét ΔBAC∆BAC và ΔBAD∆BAD có:
+) AC=ADAC=AD
+) BC=BDBC=BD
+) ABAB cạnh chung.
Suy ra ΔBAC=ΔBAD(c.c.c)∆BAC=∆BAD(c.c.c)
Suy ra ˆBACBAC^ = ˆBADBAD^ (hai góc tương ứng)
Vậy ABAB là tia phân giác của góc CADCAD.

TL :
a) Vẽ thêm các tia đối của các tia Dm, Cp, Bq và An.
Vẽ thêm các đường phân giác Ds và Ar của góc ∠D và ∠A.
Khi đó chứng minh được Cp song song với Ds.
Tương tự chứng minh được Ar song song với Dm.
Từ đó suy ra được: An // Cp và Dm // Bq.
b) Sử dụng tính chất tia phân giác của hai góc bù nhau có được Ds, Dm vuông góc với nhau.
Từ đó suy ra được: An vuông góc với Bq.
Hok tốt

Gọi số đo cạnh 1,cạnh 2,cạnh 3 lần lượt là:a,b,c(cm)(đk:a,b,c>0)
Vì cạnh 1,2,3 lần lượt tỉ lệ vs 2,3,4 nên:\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)(1)
Vì chu vi tam giác là 45cm nên:a+b+c=45(2)
Từ (1) và (2). Áp dụng tính chất dãy tỉ số = nhau:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{a+b+c}{2+3+4}=\frac{45}{9}=5\)
Vậy \(\frac{a}{2}=5\)suy ra: a=2.5=10
\(\frac{b}{3}=5\)suy ra:a=3.5=15
\(\frac{c}{4}=5\)suy ra:c=4.5=20
Vậy cạh 1 là 10cm
cạnh 2 là 15cm
cạnh 3 là 20cm



ta có: x=0,8y và y=5z(đề bài )
nên x=0,8y=0,8.5z=4z
Vậy x tỉ lệ thuận vs z theo hệ số 4
Theo điều kiện đề bài ta có:
x=0,8y và y=5z nên:
x=0,8y=0,8.5z=4z
Vậy x tỉ lệ thuận với z theo hệ số tỉ lệ là 4

a)
| t | 1 | 2 | 3 | 4 | 5 |
| s | 12 | 24 | 36 | 48 | 60 |
| \(\frac{s}{t}\) | 12 | 12 | 12 | 12 | 12 |
b)Ta có: \(\frac{s}{t}=\frac{12}{1}=\frac{24}{2}=\frac{36}{3}=\frac{48}{4}=\frac{60}{5}=12\)
\(\Rightarrow\)s=12.t\(\Rightarrow\)s tỉ lệ thuận với t theo hệ số tỉ lệ 12

Ta có:
∆ MNQ = ∆ QPM (c.c.c)
vì MN = QP (gt)
NQ = PM(gt)
MQ = QM(cạnh chung)
MN=PQ ; MP = NQ ; hai tam giác có cạnh chung là MQ
=> \(\)MN // PQ
MP // NQ