Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 2
Gọi tgv trên là tg ABC vuông tại A, AB/AC = 3/4 và AC = 125
Ta có: AB/AC = 3/4 => AB^2/AC^2 = 9/16 => 16AB^2 - 9AC^2 = 0 (*)
Ngoài ra: AC^2 = BC^2 - AB^2 = (125)^2 - AB^2 = 15625 - AB^2(**)
Thay (**) vào (*) ta có: 16AB^2 - 9(15625 - AB^2) = 0 => 25AB^2 - 140625 = 0
=> AB^2 = 5605. Vì AB > 0 => AB = 75
AC = 4/3 x AC => AC = 100
Gọi AH là là đường cao của tgv ABC, ta có BH, CH là hình chiếu của AB và AC.
Ta dễ dàng thấy tgv ABC, tgv BHA và tgv AHC là 3 tg đồng dạng, Ta có:
* BH/AB = AB/BC => BH = AB^2/BC = 75^2/125 = 45
* CH/AC = AC/BC => CH = AC^2/BC = 100^2/125 = 80
(hình bạn tự vẽ nhé)
Gọi hai hình chiếu của hai cạnh góc vuông trên cạnh huyền là x và y
Ta có : x.y = 2^2 = 4 (tích hai hình chiều bằng bình phương đường cao) (1)
và x + y = 5 => x = 5 - y
Thay vào (1) : (5 - y)y = 4 <=> y^2 - 5y + 4 = 0
<=> (x - 4)(x - 1) = 0 <=> x = 4 hoặc x = 1
=> y = 1 hoặc y = 4
Từ đó suy ra cạnh nhỏ nhất của tam giác là cạnh có hình chiếu bằng 1.
=> (cạnh gv nhỏ nhất)^2 = (hình chiếu nhỏ nhất).(cạnh huyền) = 1.5
=> cạnh góc vuông nhỏ nhất = căn 5


AB/AC=5/12
=>AB/5=AC/12=k
=>AB=5k; AC=12k
ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>25k^2+144k^2=26^2
=>169k^2=26^2
=>k^2=4
=>k=2
=>AB=10cm; AC=24cm
ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2; CH*CB=CA^2
=>BH=10^2/26=100/26=50/13(cm); CH=24^2/26=288/13(cm)
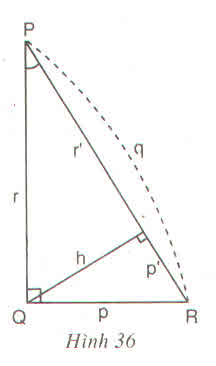
Lời giải:
a) p2 = q.p’ ; r2 = q.r’
b) 1/ h2 = 1/ p2 + 1/ r2
c) h2 =p’.r’