Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1,
\(A=1+a+\frac{1}{b}+\frac{a}{b}+1+b+\frac{1}{a}+\frac{b}{a}\)
\(\ge1+1+2\sqrt{\frac{a}{b}.\frac{b}{a}}+a+b+\frac{a+b}{ab}=4+a+b+\frac{4\left(a+b\right)}{\left(a+b\right)^2}=4+a+b+\frac{4}{a+b}\)
lại có \(\left(1+1\right)\left(a^2+b^2\right)\ge\left(a+b\right)^2\Rightarrow a+b\le\sqrt{2}\)
\(4+a+b+\frac{4}{a+b}=4+\left(a+b+\frac{2}{a+b}\right)+\frac{2}{a+b}\ge4+2\sqrt{2}+\sqrt{2}=4+3\sqrt{2}\)
\(\Rightarrow A\ge4+3\sqrt{2}\)
câu 2
ta có:\(\left(2b^2+a^2\right)\left(2+1\right)\ge\left(2b+a\right)^2\Rightarrow3c\ge a+2b\)
\(\frac{1}{a}+\frac{2}{b}=\frac{1}{a}+\frac{4}{2b}\ge\frac{9}{a+2b}\ge\frac{9}{3c}=\frac{3}{c}\left(Q.E.D\right)\)

1111111111111111111
\(VT=\Sigma\frac{xy+yz+zx}{xy}=3+\Sigma\frac{z\left(x+y\right)}{xy}\)
Đến đây để ý \(\frac{1}{2}\left[\frac{z\left(x+y\right)}{xy}+\frac{y\left(z+x\right)}{zx}\right]\ge\sqrt{\frac{\left(z+x\right)\left(x+y\right)}{x^2}}\left(\text{AM - GM}\right)\)
Là xong.

Bài ezzz =))))
\(VT=\frac{\frac{1}{a^2}}{a\left(b+c\right)}+\frac{\frac{1}{b^2}}{b\left(c+a\right)}+\frac{\frac{1}{c^2}}{c\left(a+b\right)}\)
Áp dụng bđt Bunhiacopski ta có
\(VT\ge\frac{\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2}{2\left(ab+bc+ca\right)}=\frac{\left(ab+bc+ca\right)^2}{2\left(ab+bc+ca\right)}=\frac{ab+bc+ca}{2}\ge\frac{3\sqrt[3]{a^2b^2c^2}}{2}=\frac{3}{2}\)
Dấu "=" xảy ra khi a=b=c=1
cách 2 . đặt ẩn phụ nhé bro
Đặt \(\left\{\frac{1}{a};\frac{1}{b};\frac{1}{c}\right\}\rightarrow\left\{x;y;z\right\}\)\(\Rightarrow xyz=1\), khi đó :
Bất đẳng thức cần chứng minh tương đương :\(\frac{1}{\left(\frac{1}{x}\right)^2\left(\frac{1}{y}+\frac{1}{z}\right)}+\frac{1}{\left(\frac{1}{y}\right)^2\left(\frac{1}{z}+\frac{1}{x}\right)}+\frac{1}{\left(\frac{1}{z}\right)^2\left(\frac{1}{x}+\frac{1}{y}\right)}\ge\frac{3}{2}\)
\(< =>\frac{x^3yz}{y+z}+\frac{xy^3z}{z+x}+\frac{xyz^3}{x+y}\ge\frac{3}{2}< =>\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}\ge\frac{3}{2}\)
Sử dụng bất đẳng thức AM-GM ta có : \(\left(\frac{x^2}{y+z}+\frac{y+z}{4}\right)+\left(\frac{y^2}{x+z}+\frac{x+z}{4}\right)+\left(\frac{z^2}{x+y}+\frac{x+y}{4}\right)\ge2\sqrt{\frac{x^2}{4}}+2\sqrt{\frac{y^2}{4}}+2\sqrt{\frac{z^2}{4}}=\frac{2x}{2}+\frac{2y}{2}+\frac{2z}{2}=x+y+z\)
Suy ra :\(\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}+\frac{x+y+y+z+z+x}{4}\ge x+y+z< =>\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}\ge\frac{x+y+z}{2}\)
Theo đánh giá của AM-GM thì : \(\frac{x+y+z}{2}\ge\frac{3\sqrt[3]{xyz}}{2}=\frac{3}{2}\)Từ đó ta suy ra được :
\(\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}\ge\frac{x+y+z}{2}\ge\frac{3}{2}\left(đpcm\right)\)
Dấu "=" xảy ra khi và chỉ khi \(x=y=z=1< =>a=b=c=1\)

c) Ta có: \(\left\{{}\begin{matrix}\dfrac{x+2}{x+1}+\dfrac{2}{y-2}=6\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x+1}+\dfrac{10}{y-2}=25\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{11}{y-2}=22\\\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-2=\dfrac{1}{2}\\\dfrac{1}{x+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=1\\y-2=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{5}{2}\end{matrix}\right.\)
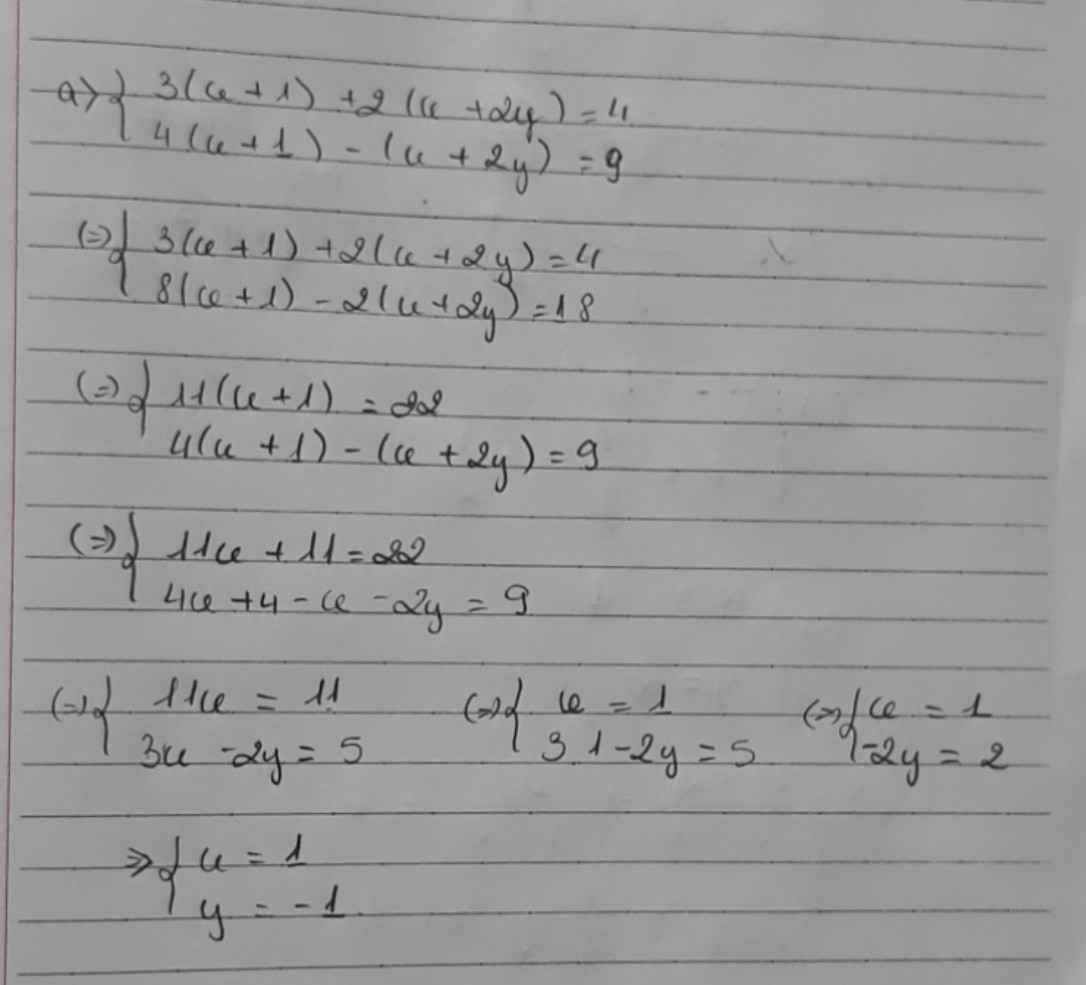
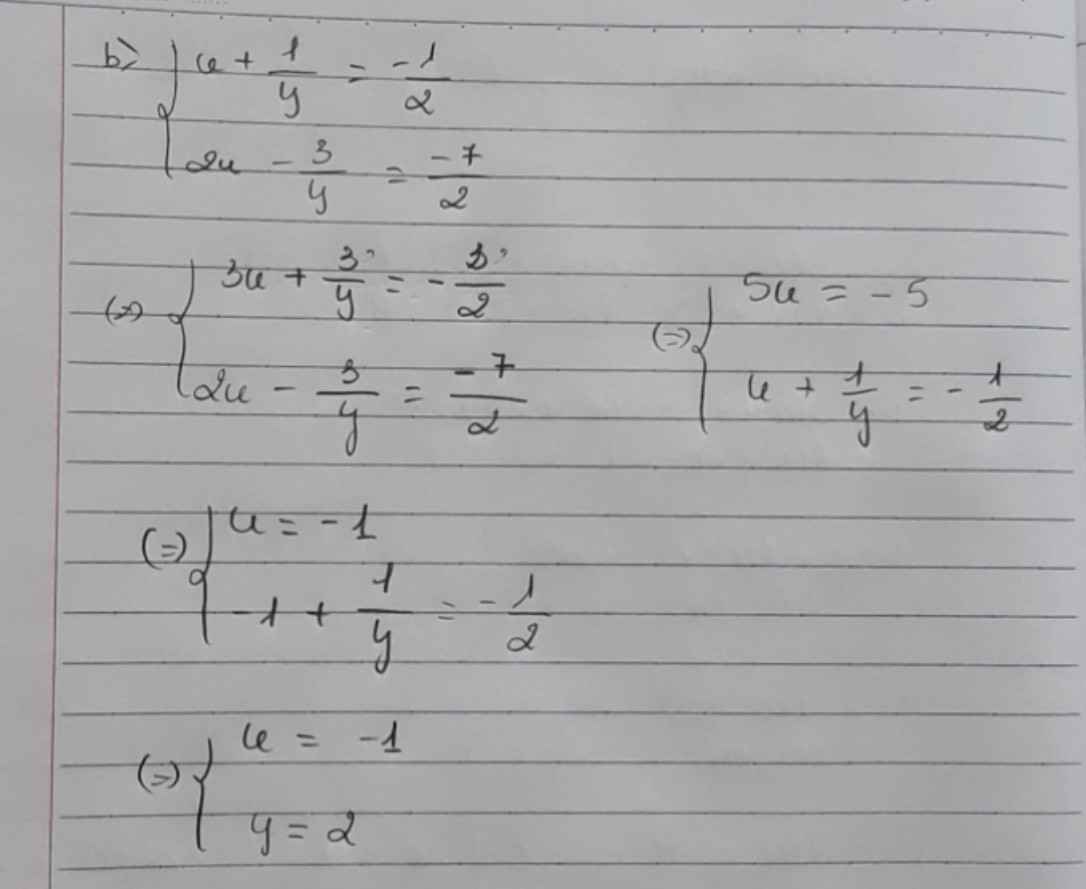
Đặt: \(a=\frac{1+x}{1-x};b=\frac{1+y}{1-y};c=\frac{1+z}{1-z}\)
\(\Rightarrow-1< x,y,z< 1\)
Theo đề bài thì \(abc=1\)
\(\Rightarrow\frac{1+x}{1-x}.\frac{1+y}{1-y}.\frac{1+z}{1-z}=1\)
\(\Rightarrow x+y+z=-xyz\)
Thế lại bài toán ta có:
\(\text{ Σ}\frac{a\left(3a+1\right)}{\left(a+1\right)^2}=\text{ Σ}\frac{\left(\frac{1+x}{1-x}\right)\left(3.\frac{1+x}{1-x}+1\right)}{\left(\frac{1+x}{1-x}+1\right)^2}=\text{ Σ}\frac{x^2+3x+2}{2}\)
\(=\frac{x^2+y^2+z^2+3\left(x+y+z\right)}{2}+3\)
\(=3+\frac{x^2+y^2+z^2-3xyz}{2}\)
\(\ge3+\frac{3\sqrt[3]{x^2y^2z^2}-3xyz}{2}\)
\(=3+\frac{3\sqrt[3]{x^2y^2z^2}.\left(1-\sqrt[3]{xyz}\right)}{2}\ge3\)
PS: Nè cô
Nè cô Bùi Thị Vân - Trang của Bùi Thị Vân - Học toán với OnlineMath