Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$x+2y=5\Leftrightarrow x=5-2y$. Thay vô pt $(1)$
$m(5-2y)+y=4$
$\Leftrightarrow y(1-2m)=4-5m$
Để pt có nghiệm duy nhất thì $1-2m\neq 0\Leftrightarrow m\neq \frac{1}{2}$
Khi đó: $y=\frac{4-5m}{1-2m}$
$x=5-2y=5-\frac{2(4-5m)}{1-2m}=\frac{-3}{1-2m}$
$x>0\Leftrightarrow \frac{-3}{1-2m}>0\Leftrightarrow 1-2m<0\Leftrightarrow m> \frac{1}{2}(1)$
$y>0\Leftrightarrow \frac{4-5m}{1-2m}>0\Leftrightarrow 4-5m<0$ (do $1-2m< 0$
$\Leftrightarrow m> \frac{4}{5}(2)$
Từ $(1); (2)\Rightarrow m> \frac{4}{5}$
$x> y\Leftrightarrow \frac{-3}{1-2m}> \frac{4-5m}{1-2m}$
$\Leftrightarrow \frac{5m-7}{1-2m}>0$
$\Leftrightarrow 5m-7< 0$ (do $1-2m<0$)
$\Leftrightarrow m< \frac{7}{5}$
Vậy $\frac{4}{5}< m< \frac{7}{5}$
Lời giải:
$x+2y=5\Leftrightarrow x=5-2y$. Thay vô pt $(1)$
$m(5-2y)+y=4$
$\Leftrightarrow y(1-2m)=4-5m$
Để pt có nghiệm duy nhất thì $1-2m\neq 0\Leftrightarrow m\neq \frac{1}{2}$
Khi đó: $y=\frac{4-5m}{1-2m}$
$x=5-2y=5-\frac{2(4-5m)}{1-2m}=\frac{-3}{1-2m}$
$x>0\Leftrightarrow \frac{-3}{1-2m}>0\Leftrightarrow 1-2m<0\Leftrightarrow m> \frac{1}{2}(1)$
$y>0\Leftrightarrow \frac{4-5m}{1-2m}>0\Leftrightarrow 4-5m<0$ (do $1-2m< 0$
$\Leftrightarrow m> \frac{4}{5}(2)$
Từ $(1); (2)\Rightarrow m> \frac{4}{5}$
$x> y\Leftrightarrow \frac{-3}{1-2m}> \frac{4-5m}{1-2m}$
$\Leftrightarrow \frac{5m-7}{1-2m}>0$
$\Leftrightarrow 5m-7< 0$ (do $1-2m<0$)
$\Leftrightarrow m< \frac{7}{5}$
Vậy $\frac{4}{5}< m< \frac{7}{5}$

Ta có: \(\left\{{}\begin{matrix}x+my=2\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\m\left(2-my\right)-2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\2m-m^2y-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\2m-\left(m^2y+2y\right)=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\m^2y+2y=2m-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\y\left(m^2+2\right)=2m-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2-my\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2-\dfrac{m\cdot\left(2m-1\right)}{m^2+2}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2m^2+4-2m^2+m}{m^2+2}=\dfrac{m+4}{m^2+2}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
Tới đây bạn tự làm tiếp nhé

Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{1}{m}\ne\dfrac{m}{1}\)
=>\(m^2\ne1\)
=>\(m\notin\left\{1;-1\right\}\)
Khi \(m\notin\left\{1;-1\right\}\) thì \(\left\{{}\begin{matrix}x+my=m+1\\mx+y=2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\m\left(m+1-my\right)+y=2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m+1-my\\m^2+m-m^2y+y-2m=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y\left(-m^2+1\right)=-m^2+m\\x=m+1-my\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m^2-m}{m^2-1}=\dfrac{m\left(m-1\right)}{\left(m-1\right)\left(m+1\right)}=\dfrac{m}{m+1}\\x=m+1-\dfrac{m^2}{m+1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m}{m+1}\\x=\dfrac{\left(m+1\right)^2-m^2}{m+1}=\dfrac{2m+1}{m+1}\end{matrix}\right.\)
Để \(\left\{{}\begin{matrix}x>=2\\y>=1\end{matrix}\right.\) thì \(\left\{{}\begin{matrix}\dfrac{2m+1}{m+1}>=2\\\dfrac{m}{m+1}>=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2m+1-2\left(m+1\right)}{m+1}>=0\\\dfrac{m-m-1}{m+1}>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2m+1-2m-2}{m+1}>=0\\\dfrac{-1}{m+1}>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-\dfrac{1}{m+1}>=0\\-\dfrac{1}{m+1}>=0\end{matrix}\right.\Leftrightarrow m+1< 0\)
=>m<-1

Để hệ pt có một nghiệm duy nhất thì \(\dfrac{m}{4}\ne\dfrac{1}{m}\Leftrightarrow2m\ne4\Leftrightarrow m\ne2\)
Từ pt 1 ta có: y=mx-1 thế vào pt 2 ta đc:
4x-m(mx-1)=2
\(\Leftrightarrow4x-m^2x+m=2\)
\(\Leftrightarrow\left(4-m^2\right)x=2-m\) (*)
Để hệ có nghiệm duy nhất thì pt (*) phải óc nghiệm duy nhất
tức \(4-m^2\ne0\Leftrightarrow m^2\ne4\Leftrightarrow m\ne\pm2\)
Vây \(m\ne\pm2\) thì hệ có nghiệm duy nhất

a. Với `m=1`, ta có HPT: \(\left\{{}\begin{matrix}x+2y=18\\x-y=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-6\\3y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=8\end{matrix}\right.\)
b. Theo đề bài `=>` \(\left\{{}\begin{matrix}mx+2y=18\\x-y=-6\\2x+y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}mx+2y=18\\x=1\\y=7\end{matrix}\right.\)
`=> m=4`

Kết hợp điều kiện đề bài và pt thứ 2 của hệ ta được:
\(\left\{{}\begin{matrix}x-y=-6\\2x+y=9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=7\end{matrix}\right.\)
Thế vào pt đầu:
\(m.1+2.7=18\Rightarrow m=4\)

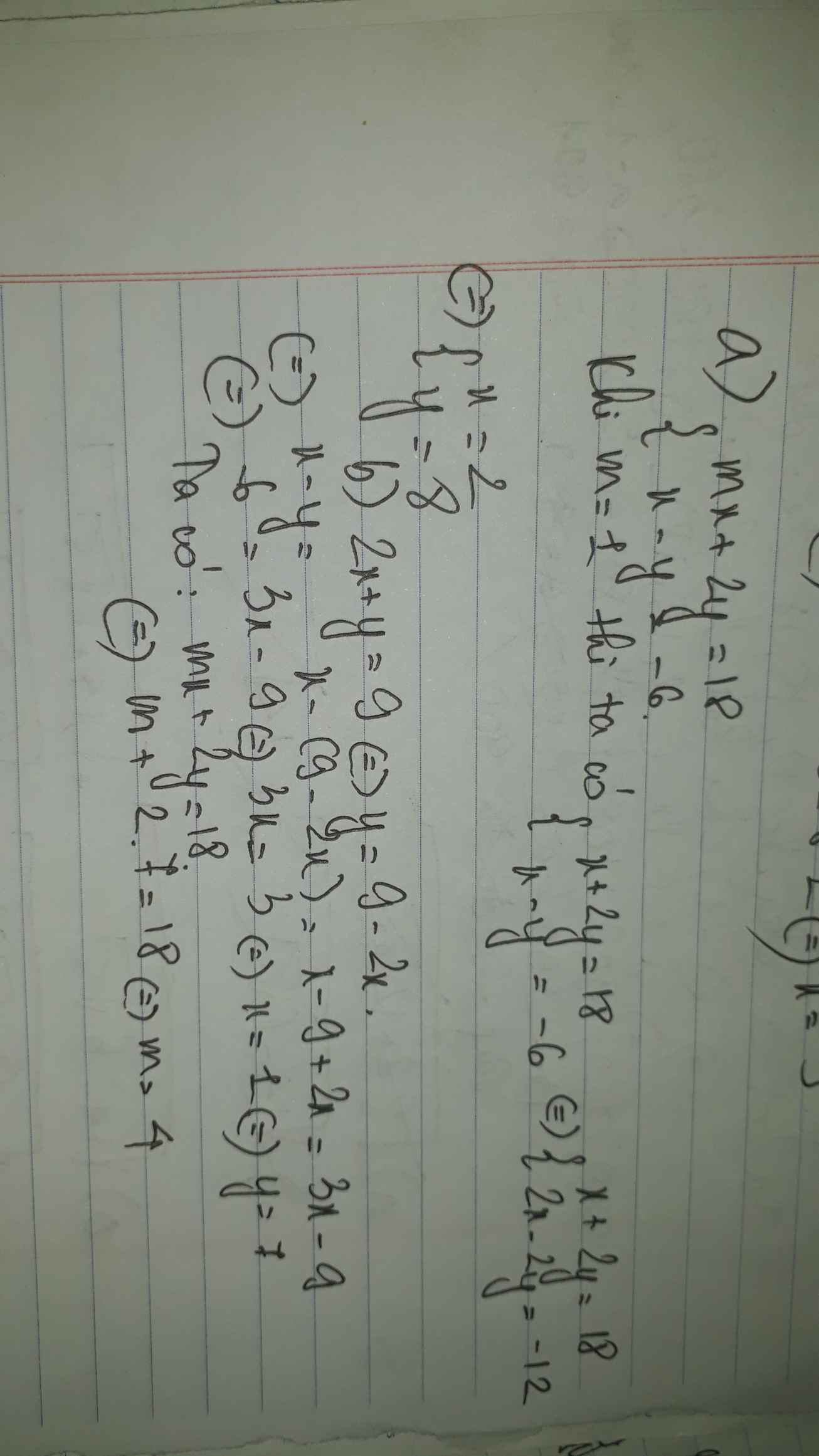
Để hệ có nghiệm duy nhât thì m/1<>-2/-m
=>m^2<>2
=>\(m\ne\pm\sqrt{2}\)