Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta tính các định thức:
D = m 1 1 m = m 2 - 1 = m + 1 . m - 1 ; D x = m + 1 1 2 m = m 2 + m - 2 = m - 1 . m + 2 ; D y = m m + 1 1 2 = m - 1
Xét D = 0 tức là m = 1 hoặc m = -1.
* Nếu m = 1 thì D = Dx = Dy = 0 nên hệ phương trình đã cho có vô số nghiệm.
Do đó, a= 1.
* Nếu m = -1 thì D = 0 nhưng D x ≠ 0 nên hệ phương trình đã cho vô nghiệm.
Do đó, b = -1
Tổng a+ b = 0.
Chọn A.

Đặt \(x+\dfrac{1}{x}=a;y+\dfrac{1}{y}=b\left(\left|a\right|\ge2;\left|b\right|\ge2\right)\)
\(\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\x^3+y^3+\dfrac{1}{x^3}+\dfrac{1}{y^3}=15m-25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\\left(x^3+\dfrac{1}{x^3}\right)+\left(y^3+\dfrac{1}{y^3}\right)=15m-25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\\left(x+\dfrac{1}{x}\right)^3-3\left(x+\dfrac{1}{x}\right)+\left(y+\dfrac{1}{y}\right)^3-3\left(y+\dfrac{1}{y}\right)=15m-25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\\left(x+\dfrac{1}{x}\right)^3+\left(y+\dfrac{1}{y}\right)^3-3\left(x+\dfrac{1}{x}+y+\dfrac{1}{y}\right)=15m-25\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}+y+\dfrac{1}{y}=5\\\left(x+\dfrac{1}{x}\right)^3+\left(y+\dfrac{1}{y}\right)^3=15m-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\a^3+b^3=15m-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\\left(a+b\right)^3-3ab\left(a+b\right)=15m-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\125-15ab=15m-10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=5\\ab=9-m\end{matrix}\right.\)
\(\Rightarrow a,b\) là nghiệm của phương trình \(t^2-5t+9-m=0\left(1\right)\)
a, Nếu \(m=3\), phương trình \(\left(1\right)\) trở thành
\(t^2-5t+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2\\t=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\\\left\{{}\begin{matrix}a=3\\b=2\end{matrix}\right.\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x+\dfrac{1}{x}=2\\y+\dfrac{1}{y}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)^2=0\\y^2-3y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3\pm\sqrt{5}}{2}\end{matrix}\right.\)
TH2: \(\left\{{}\begin{matrix}x+\dfrac{1}{x}=3\\y+\dfrac{1}{y}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3\pm\sqrt{5}}{2}\\y=1\end{matrix}\right.\)
Vậy ...
b, \(\left(1\right)\Leftrightarrow t=\dfrac{5\pm\sqrt{4m-11}}{2}\left(m\ge\dfrac{11}{4}\right)\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{5\pm\sqrt{4m-11}}{2}\\b=\dfrac{5\mp\sqrt{4m-11}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\dfrac{1}{x}=\dfrac{5\pm\sqrt{4m-11}}{2}\\y+\dfrac{1}{y}=\dfrac{5\mp\sqrt{4m-11}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x^2-\left(5\pm\sqrt{4m-11}\right)+2=0\left(2\right)\\2y^2-\left(5\mp\sqrt{4m-11}\right)+2=0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(\left(2\right)\) có nghiệm dương
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(5\pm\sqrt{4m-11}\right)^2-16\ge0\\\dfrac{5\pm\sqrt{4m-11}}{2}>0\\1>0\end{matrix}\right.\)
\(\Leftrightarrow...\)

Ta có: D = 1 − m m − 1 = m 2 − 1 ; D x = 0 − m m + 1 − 1 = m ( m + 1 ) ; D y = 1 0 m m + 1 = m + 1
Nếu D = 0 ⇔ m 2 - 1 = 0 ⇔ m = ± 1
Với m = 1 ⇒ D x ≠ 0 nên hệ phương trình vô nghiệm.
Với m = - 1 ⇒ D x = D y = 0 nên hệ phương trình có vô số nghiệm.
Đáp án cần chọn là: C

Ta có: D = 2 − 1 1 2 = 5 ≠ 0
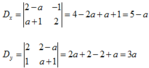
Vì D ≠ 0 nên hệ phương trình có nghiệm duy nhất
x = D x D = 5 − a 5 ; y = D y D = 3 a 5
Khi đó:
x 2 + y 2 = 5 − a 5 2 + 3 a 5 2
= 25 − 10 a + 10 a 2 25 = 10 25 a 2 − a + 1 = 2 5 a − 1 2 2 + 9 10 ≥ 9 10
Dấu “=” xảy ra ⇔ a = 1 2
Đáp án cần chọn là: C

Ta có: D = 2 m + 1 1 m 2 − 1 = − 2 m − 1 − m 2 = − m + 1 2
D x = 2 m − 2 1 m 2 − 3 m − 1
= − 2 m + 2 − m 2 + 3 m = − m 2 + m + 2 = m + 1 2 − m
D y = 2 m + 1 2 m − 2 m 2 m 2 − 3 m = 2 m + 1 m 2 − 3 m − m 2 2 m − 2
= − 3 m 2 − 3 m = − 3 m m + 1
Nếu m ≠ − 1 thì hệ phương trình có nghiệm duy nhất
x = D x D = m − 2 m + 1 = 1 − 3 m + 1 y = D y D = 3 m m + 1 = 3 − 3 m + 1
Để x , y ∈ Z suy ra 3 m + 1 ∈ Z , m + 1 ∈ U , ( 3 ) = ± 1 ; ± 3
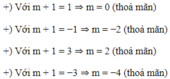
Vậy có 4 giá trị của m thoả mãn đề bài.
Đáp án cần chọn là: D

Ta có D = m − 1 2 m = m 2 + 2 > 0 , ∀ m ∈ R nên hệ phương trình luôn có nghiệm duy nhất
D x = 3 − 1 9 m = 3 m + 9 ; D y = m 3 2 9 = 9 m − 6
Vậy hệ luôn có nghiệm duy nhất là: x = 3 m + 9 m 2 + 2 y = 9 m − 6 m 2 + 2
Ta có: A = 3 x − y = 3 3 m + 9 m 2 + 2 − 9 m − 6 m 2 + 2 = 33 m 2 + 2
Vì m ∈ Z nên để A nguyên thì m 2 + 2 là ước của 33 mà m 2 + 2 ≥ 2 nên ta có các trường hợp sau:

Mà m nguyên dương nên m ∈ 1 ; 3
Vậy có 2 giá trị nguyên dương của m để A nguyên.
Đáp án cần chọn là: B
Ta có: D = a 1 6 b = a b − 6 ; D x = 2 1 4 b = 2 b − 4 ; D y = a 2 6 4 = 4 a − 12
Hệ phương trình vô nghiệm ⇔ D = 0 D x ≠ 0 D y ≠ 0 ⇔ a b = 6 b ≠ 2 a ≠ 3
Vì 6 = 1 . 6 = 6 .1 = (−1). (−6) = (−6). (−1) = 2.3 = 3.2 = (−2). (−3) = (−3). (−2)
Vậy có 7 cặp (a,b) thoả mãn đề bài.
Đáp án cần chọn là: A