Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: (SB;(ABC))=(BS;BA)=góc SBA
BA^2+BC^2=AC^2
=>2*BA^2=AC^2
=>AB=BC=a
tan SBA=SA/SB=căn 3
=>góc SBA=60 độ
d: (SB;(BAC))=(BS;BA)=góc SBA=60 độ
e:
CB vuông góc AB
CB vuông góc SA
=>CB vuông góc (SBA)
=>(SC;(SBA))=(SC;SB)=góc BSC
SB=căn SA^2+AB^2=2a
SC=căn SA^2+AC^2=a*căn 5
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
sin BSC=BC/SC=a/a*căn 5=1/căn 5
=>góc BSC\(\simeq27^0\)

Phần góc giữa 2 mặt phẳng tui chưa học đến nên chưa làm được đoạn cuối phần b, bạn thông cảm nha!


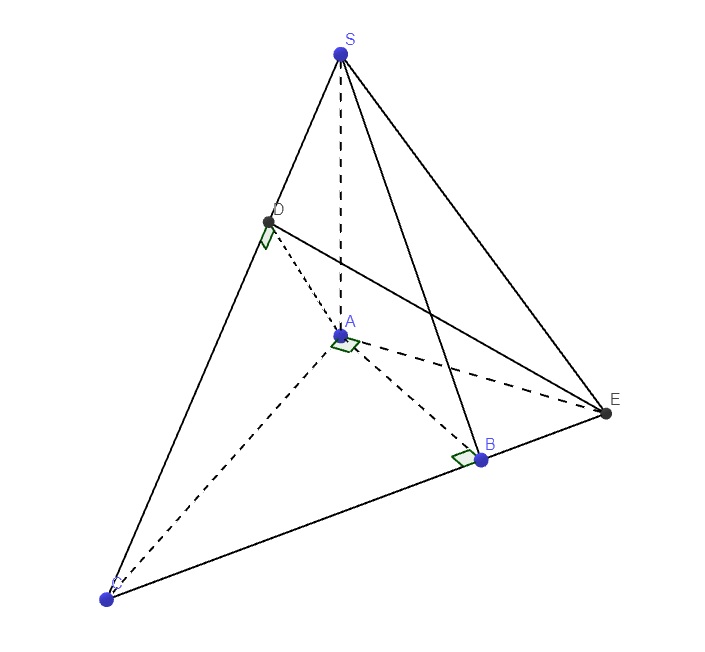
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)

a: (SB;(ABC))=(SB;BA)=góc SBA
\(\tan SBA=\dfrac{SA}{AB}=\sqrt{6}\)
=>góc SBA=68 độ
b: (SA;(SBC))=(SA;SB)=góc ASB
tan ASB=AB/SA=1/căn 6
=>góc ASB=22 độ

Trong mp (SAC), từ A kẻ \(AD\perp SC\) (D thuộc SC) (1)
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AC cắt BC kéo dài tại E
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp AE\\AE\perp AC\end{matrix}\right.\) \(\Rightarrow AE\perp\left(SAC\right)\Rightarrow\left\{{}\begin{matrix}AE\perp AE\\AE\perp SC\left(2\right)\end{matrix}\right.\)
(1);(2) \(\Rightarrow SC\perp\left(ADE\right)\)
Mà \(SC=\left(SAC\right)\cap\left(SBC\right)\Rightarrow\widehat{ADE}\) là góc giữa (SAC) và (SBC)
\(AC=\sqrt{AB^2+BC^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{AD^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AD=\dfrac{2a\sqrt{33}}{11}\)
\(\dfrac{1}{AB^2}=\dfrac{1}{AC^2}+\dfrac{1}{AE^2}\Rightarrow AE=\dfrac{AB.AC}{\sqrt{AC^2-AB^2}}=\dfrac{2a\sqrt{3}}{3}\)
\(\Rightarrow tan\widehat{ADE}=\dfrac{AE}{AD}=...\)
1.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SA lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC là (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{5}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{\sqrt{15}}{5}\Rightarrow\widehat{SCA}\approx37^045'\)
b.
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(\left\{{}\begin{matrix}BC=\left(SBC\right)\cap\left(ABC\right)\\SB=\left(SBC\right)\cap\left(SAB\right)\\AB=\left(ABC\right)\cap\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{3}\Rightarrow\widehat{SBA}=60^0\)
c.
Trong mp (SAB), từ A kẻ \(AH\perp SB\)
Mà \(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\)
\(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{3}}{2}\)
2.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB là (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=3\Rightarrow\widehat{SBA}\approx71^034'\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(\left\{{}\begin{matrix}BC=\left(SBC\right)\cap\left(ABCD\right)\\SB=\left(SAB\right)\cap\left(SBC\right)\\AB=\left(SAB\right)\cap\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABCD) (đã tính ở câu a)
c.
Từ A kẻ \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{3a\sqrt{10}}{10}\)