Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gợi ý: Chứng minh QCGA và CRDP là hình bình hành;
b) Chứng minh DQCM = DGAB để suy ra QRGP là hình bình hành;
c) Có
S R C B = 1 3 . S B C D = 1 6 . S A B C D
Và
S C G D = 1 3 . S A C D = 1 6 . S A B C D Þ ĐPCM.
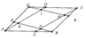

a: Xét tứ giác AKCQ có
AK//CQ
AK=CQ
Do đó: AKCQ là hình bình hành

a: Xét ΔBAC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//AC
Xét tứ giác AMNC có MN//AC
nên AMNC là hình thang
b: Xét tứ giác MBCP có
MB//CP
MB=CP
Do đó: MBCP là hình bình hành
a: Xét tứ giác PBRD có
PB//RD
PB=RD
DO đó: PBRD là hình bình hành
b: Xét tứ giác AQCS có
AS//CQ
AS=CQ
DO đó: AQCS là hình bình hành
=>AQ//SC
=>KI//MN
Xét tứ giác MNKI có
MN//KI
MI//KN
DO đó: MNKI là hình bình hành