PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Từ đồ thị hàm số ta thấy khi x tăng từ -3 đến -1 và từ -1 đến 0 thì đồ thị đi lên nên hàm số đồng biến trên các khoảng (-3;-1) và (-1;0).
Khi x tăng từ 0 đến 2 thì đồ thị đi xuống nên hàm số nghịch biến trên (0;2).
CM
19 tháng 5 2018
Với x > 0 ta có đồ thị của y = f | ( x ) | như hình 41 (bỏ phần ứng với x ≤ 0)
Với x ≤ 0, trước hết vẽ đồ thị hàm số y = 2x + 2. Giữ yên phần đồ thị đoạn [-1;0], bỏ đi phần đồ thị ứng với khoảng ( - ∞ ; - 1 ) , thay vào đó là phần đối xứng với phần bỏ đi qua trục hoành. Đồ thị hàm số y = f | ( x ) | được vẽ trên hình 42 (đường nét liền).
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
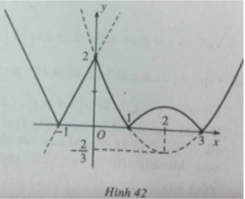
a) Quan sát đồ thị:
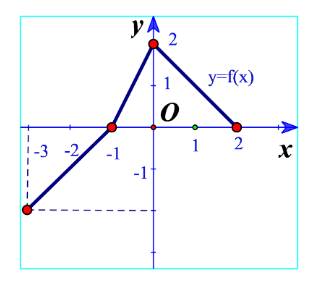
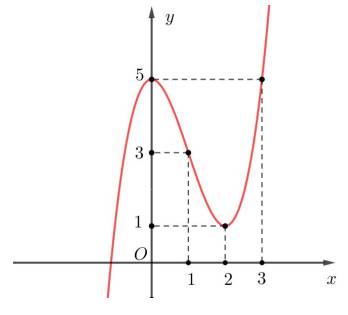
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
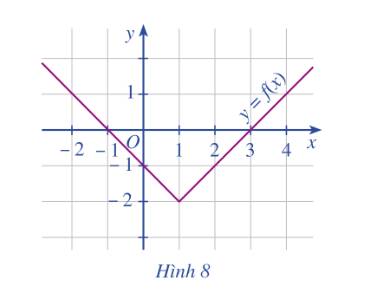
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).
CM
31 tháng 3 2018
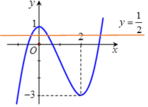
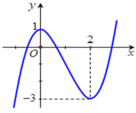
Phương trình đã cho tương đương f x = 1 2
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f x và đường thẳng y = 1 2
Quan sát đồ thị hàm số ta thấy đường thẳng y = 1 2 cắt đồ thị hàm số y = f x tại đúng 3 điểm phân biệt.
Vậy phương trình 2 f x - 1 = 0 có 3 nghiệm phân biệt.
Đáp án cần chọn là: B
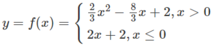
Hình vẽ??