Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: 
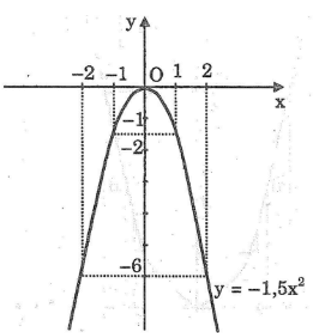
b: Vì a=-1,5<0 nên hàm số đồng biến khi x<0 và nghịch biến khi x>0
=>f(-1,5)< f(-0,5) và f(0,75)>f(1,5)
- Khi 1 ≤ x ≤ 2 thì -6 ≤ y ≤ -1,5 ;
- Khi -2 ≤ x ≤ 0 thì -6 ≤ y ≤ 0 ;
- Khi -2 ≤ x ≤ 1 thì -6 ≤ y ≤ 0.
Đặt \(X=x+1\)
Khi đó, hàm số \(y=f\left(x\right)=g\left(X\right)=X^2\)có dạng \(y=ax^2\)
Với \(-2\le x\le2\)thì \(-1\le X\le3\)
Vì \(a=1>0\)nên hàm số đồng biến khi \(X>0\); nghịch biến khi \(X< 0\)và đạt giá trị nhỏ nhất là \(y=0\)tại \(X=0\)
+ Xét \(-1\le X\le0\), hàm số nghịch biến nên ta có :
\(g\left(-1\right)\ge g\left(X\right)\ge g\left(0\right)\Leftrightarrow1\ge f\left(x\right)\ge0\)
+ Xét \(0\le X\le3\), hàm số đồng biến nên ta có :
\(g\left(0\right)\le g\left(X\right)\le g\left(3\right)\Leftrightarrow0\le f\left(x\right)\le9\)Suy ra với \(-2\le x\le2\)thì \(0\le f\left(x\right)\le9\)
Câu 1:
ĐKXĐ: x<>2
Lấy x1,x2 sao cho \(x_1< x_2\)
\(A=\dfrac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}=\left(\dfrac{x_1+1}{x_1-2}-\dfrac{x_2+1}{x_2-2}\right):\left(x_1-x_2\right)\)
\(=\dfrac{x_1x_2-2x_1+x_2-2-x_1x_2+2x_2-x_1+2}{\left(x_1-2\right)\left(x_2-2\right)}\cdot\dfrac{1}{x_1-x_2}\)
\(=\dfrac{-2\left(x_1-x_2\right)-\left(x_1-x_2\right)}{\left(x_1-2\right)\left(x_2-2\right)}\cdot\dfrac{1}{x_1-x_2}=\dfrac{-3}{\left(x_1-2\right)\left(x_2-2\right)}\)
TH1: \(x_1< 2;x_2< 2\)
\(\Leftrightarrow\left(x_1-2\right)\left(x_2-2\right)>0\)
=>A<0
=>Hàm số nghịch biến khi x<2
TH2: \(x_1>2;x_2>2\)
\(\Leftrightarrow\left(x_1-2\right)\left(x_2-2\right)>0\)
=>A<0
=>Hàm số nghịch biến khi x>2
Ta có :
- Khi 1 ≤ x ≤ 2 thì -6 ≤ y ≤ -1,5 ;
- Khi -2 ≤ x ≤ 0 thì -6 ≤ y ≤ 0 ;
- Khi -2 ≤ x ≤ 1 thì -6 ≤ y ≤ 0.
bạn ấn vào đúng 0 sẽ ra kết quả, mình giải được rồi dễ lắm