Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cách 1: Ta có:
y' = 6sin5x.cosx - 6cos5x.sinx + 6sinx.cos3x - 6sin3x.cosx = 6sin3x.cosx(sin2x - 1) + 6sinx.cos3x(1 - cos2x) = - 6sin3x.cos3x + 6sin3x.cos3x = 0.
Vậy y' = 0 với mọi x, tức là y' không phụ thuộc vào x.
Cách 2:
y = sin6x + cos6x + 3sin2x.cos2x(sin2x + cos2x) = sin6x + 3sin4x.cos2x + 3sin2x.cos4x + cos6x = (sin2x + cos2x)3 = 1
Do đó, y' = 0.
b) Cách 1:
Áp dụng công thức tính đạo hàm của hàm số hợp
(cos2u)' = 2cosu(-sinu).u' = -u'.sin2u
Ta được
y' =[sin - sin
] + [sin
- sin
] - 2sin2x = 2cos
.sin(-2x) + 2cos
.sin(-2x) - 2sin2x = sin2x + sin2x - 2sin2x = 0,
vì cos = cos
=
.
Vậy y' = 0 với mọi x, do đó y' không phụ thuộc vào x.
Cách 2: vì côsin của hai cung bù nhau thì đối nhau cho nên
cos2 = cos2
'
cos2 = cos2
.
Do đó
y = 2 cos2 + 2cos2
- 2sin2x = 1 +cos
+ 1 +cos
- (1 - cos2x) = 1 +cos
+ cos
+ cos2x = 1 + 2cos
.cos(-2x) + cos2x = 1 + 2
cos2x + cos2x = 1.
Do đó y' = 0.

1. Ta có: \(-1\le sinx\le1\)
\(\Rightarrow-3\le y\le3\) (hàm đã cho đồng biến trên \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
\(y_{min}=-3\) khi \(sinx=-1\)
\(y_{max}=3\) khi \(sinx=1\)
2.
\(y=1-sin^2x-2sinx=2-\left(sinx+1\right)^2\)
Do \(-1\le sinx\le1\Rightarrow0\le sinx+1\le2\)
\(\Rightarrow-2\le y\le2\)
\(y_{min}=-2\) khi \(sinx=1\)
\(y_{max}=2\) khi \(sinx=-1\)
3.
\(y=1-cos^2x+cos^4x=\left(cos^2x-\frac{1}{2}\right)^2+\frac{3}{4}\)
\(\Rightarrow y\ge\frac{3}{4}\Rightarrow y_{min}=\frac{3}{4}\) khi \(cos^2x=\frac{1}{2}\)
\(y=1+cos^2x\left(cos^2x-1\right)\le1\) do \(cos^2x-1\le0\)
\(\Rightarrow y_{max}=1\) khi \(\left[{}\begin{matrix}cos^2x=1\\cos^2x=0\end{matrix}\right.\)
4.
\(y=\left(sin^2x+cos^2x\right)^2-2\left(sinx.cosx\right)^2+sinx.cosx\)
\(y=1-\frac{1}{2}sin^22x+\frac{1}{2}sin2x\)
\(y=\frac{9}{8}-\frac{1}{2}\left(sinx-\frac{1}{2}\right)^2\le\frac{9}{8}\)
\(y_{max}=\frac{9}{8}\) khi \(sinx=\frac{1}{2}\)
\(y=\frac{1}{2}\left(sinx+1\right)\left(2-sinx\right)\ge0;\forall x\)
\(\Rightarrow y_{min}=0\) khi \(sinx=-1\)

Bài 1:
ĐK : sinx cosx > 0
Khi đó phương trình trở thành
sinx+cosx=\(2\sqrt{\sin x\cos x}\)
ĐK sinx + cosx >0 → sinx>0 ; cosx>0
Khi đó \(2\sqrt{\sin x\cos x}\Leftrightarrow2\sin x=1\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
Vậy ...
Bài 2:
ĐK : \(\sin\left(3x+\frac{\pi}{4}\right)\ge0\)
Khi đó phương trình đã cho tương đương với phương trình \(\sin2x=\frac{1}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\frac{\pi}{12}+k\pi\\x=\frac{5\pi}{12}+k\pi\end{matrix}\right.\)
Trong khoảng từ \(\left(-\pi,\pi\right)\) ta nhận được các giá trị :
\(x=\frac{\pi}{12}\) (TMĐK)
\(x=-\frac{11\pi}{12}\) (KTMĐK)
\(x=\frac{5\pi}{12}\) (KTMĐK)
\(x=-\frac{7\pi}{12}\) (TMĐK)
Vậy ta có 2 nghiệm thõa mãn \(x=\frac{\pi}{12}\) và \(x=-\frac{7\pi}{12}\)
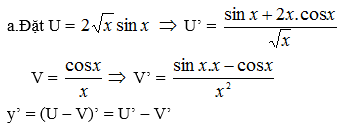
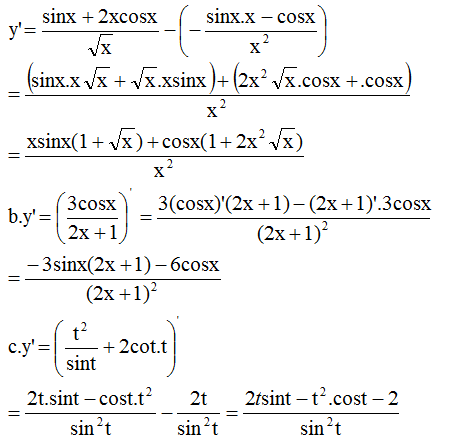
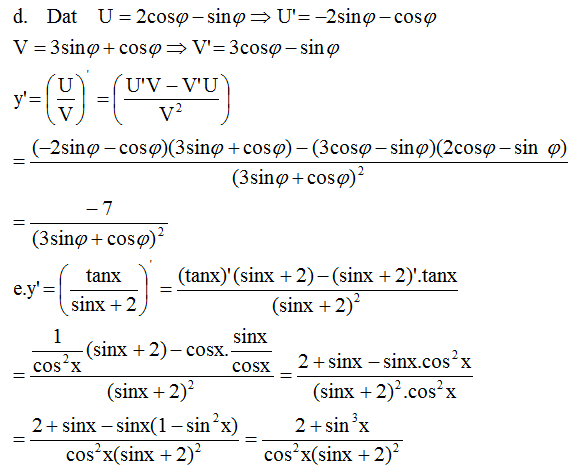
\(D=R\backslash\left\{0\right\}\)
\(\sin^3x+\cos^3x=\left(\sin x+\cos x\right)\left(\sin^2x-\sin x\cos x+\cos^2x\right)=\left(\sin x+\cos x\right)\left(1-\sin x\cos x\right)\)
\(2-\sin2x=2-2\sin x\cos x=2\left(1-\sin x\cos x\right)\)
\(\Rightarrow y=\dfrac{\left(\sin x+\cos x\right)\left(1-\sin x\cos x\right)}{2\left(1-\sin x\cos x\right)}=\dfrac{\sin x+\cos x}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}y'=\dfrac{2\cos x-2\sin x}{4}=\dfrac{1}{2}\left(\cos x-\sin x\right)\Rightarrow y'^2=\dfrac{1}{4}\left(\cos^2x-2\sin x\cos x+\sin^2x\right)=\dfrac{1}{4}\left(1-2\sin x\cos x\right)\\y''=-\dfrac{1}{2}.\sin x-\dfrac{1}{2}\cos x\Rightarrow y''^2=\left[-\dfrac{1}{2}\left(\sin x+\cos x\right)\right]^2=\dfrac{1}{4}\left(1+2\sin x\cos x\right)\end{matrix}\right.\)
\(\Rightarrow2\left(y'^2+y''^2\right)=2\left[\dfrac{1}{4}\left(1-\sin2x\right)+\dfrac{1}{4}\left(1+\sin2x\right)\right]=1\)