Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\left(2m-1\right)sinx-\left(m+2\right)cosx+4m-3\ge0\) ;\(\forall x\)
\(\Leftrightarrow m\ge\dfrac{sinx+2cosx+3}{2sinx-cosx+4}=P\)
\(\Leftrightarrow m\ge P_{max}\)
Ta có: \(P=\dfrac{sinx+2cosx+3}{2sinx-cosx+4}\Leftrightarrow\left(2P-1\right)sinx-\left(P+2\right)cosx=3-4P\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(3-4P\right)^2\)
\(\Leftrightarrow11P^2-24P+4\le0\)
\(\Rightarrow\dfrac{2}{11}\le P\le2\)
\(\Rightarrow m\ge2\)

để hàm số xác định với mọi x thuộc R thì
\(2m\cos^2x+\left(2-m\right)\cos x+4m-1\ge0\Leftrightarrow m\left(2cos^2x-cosx+4\right)\ge1-2cosx\)
mà \(2cos^2x-cosx+4>0\) nên :
\(m\ge\frac{1-2cosx}{2cos^2x-cosx+4}\)\(\Leftrightarrow\)\(m\ge max\left(\frac{1-2cosx}{2cos^2x-cosx+4}\right)=\frac{3}{7}\)
vậy điều kiện của m là : \(m\ge\frac{3}{7}\)

y = \(\dfrac{sin^2x}{cosx\left(sinx-cosx\right)}+\dfrac{1}{4}\)
y = \(\dfrac{sin^2x}{sinx.cosx-cos^2x}+\dfrac{1}{4}=\dfrac{\dfrac{sin^2x}{cos^2x}}{\dfrac{sinx.cosx}{cos^2x}-1}+\dfrac{1}{4}\)
y = \(\dfrac{tan^2x}{tanx-1}+\dfrac{1}{4}\)
y = \(\dfrac{4tan^2x+tanx-1}{4tanx-4}\). Đặt t = tanx. Do x ∈ \(\left(\dfrac{\pi}{4};\dfrac{\pi}{2}\right)\) nên t ∈ (1 ; +\(\infty\))\
Ta đươc hàm số f(t) = \(\dfrac{4t^2+t-1}{4t-4}\)
⇒ ymin = \(\dfrac{17}{4}\) khi t = 2. hay x = arctan(2) + kπ

Đặt \(t=cosx;t\in\left[-1;1\right]\)
Để hàm số có tập xác định R
\(\Leftrightarrow cosx^2-\left(2+m\right)cosx+2m\ge0;\forall x\)
\(\Leftrightarrow t^2-\left(2+m\right)t+2m\ge0\) với mọi \(t\in\left[-1;1\right]\)
Đặt \(f\left(t\right)=t^2-\left(2+m\right)t+2m\); \(I\left(\dfrac{2+m}{2};f\left(\dfrac{2+m}{2}\right)\right)\)
TH1: \(\dfrac{2+m}{2}< -1\) \(\Leftrightarrow m< -4\)
Để \(f\left(t\right)\ge0;\forall t\in\left[-1;1\right]\) \(\Leftrightarrow\)\(f\left(t\right)_{min}=f\left(-1\right)\ge0\) \(\Leftrightarrow3+3m\ge0\Leftrightarrow m\ge-1\)(ktm đk)
TH2: \(-1\le\dfrac{m+2}{2}\le1\)\(\Leftrightarrow-4\le m\le0\)
Để \(f\left(t\right)\ge0;\forall t\in\left[-1;1\right]\) \(\Leftrightarrow f\left(t\right)_{min}=f\left(\dfrac{2+m}{2}\right)\ge0\)\(\Leftrightarrow-m^2+4m-4\ge0\)\(\Leftrightarrow m=2\) (ktm đk)
TH3:\(\dfrac{m+2}{2}>1\) \(\Leftrightarrow m>0\)
Để \(f\left(t\right)\ge0;\forall t\in\left[-1;1\right]\)\(\Leftrightarrow f\left(t\right)_{min}=f\left(1\right)\ge0\)\(\Leftrightarrow m-1\ge0\Leftrightarrow m\ge1\)
Kết hợp cả ba TH \(\Rightarrow m\ge1\)
Vậy...
Đơn giản hơn:
\(t^2-\left(m+2\right)t+2m\ge0\) ; \(\forall t\in\left[-1;1\right]\)
\(\Leftrightarrow t\left(t-2\right)-m\left(t-2\right)\ge0\)
\(\Leftrightarrow\left(t-m\right)\left(t-2\right)\ge0\) (1)
Do \(t-2< 0\) ; \(\forall t\in\left[-1;1\right]\) nên (1) tương đương:
\(t-m\le0\)
\(\Leftrightarrow m\ge t\) ; \(\forall t\in\left[-1;1\right]\)
\(\Rightarrow m\ge1\)

1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)

a.
\(\Leftrightarrow m-cosx\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge max\left(cosx\right)\)
\(\Leftrightarrow m\ge1\)
b.
\(\Leftrightarrow2sinx-m\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\le2sinx\) ; \(\forall x\)
\(\Leftrightarrow m\le\min\limits_{x\in R}\left(2sinx\right)\)
\(\Leftrightarrow m\le-2\)
c.
\(\Leftrightarrow cosx+m\ne0\) ; \(\forall x\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\max\limits_R\left(cosx\right)\\m< \min\limits_R\left(cosx\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)

\(2sinx+5cosx-13< 0;\forall x\)
\(\Rightarrow\) Hàm xác định trên R khi và chỉ khi:
\(2m.sinx+\left(2m-1\right)cosx-m< 0\) ;\(\forall x\)
\(\Leftrightarrow2m.sinx+\left(2m-1\right).cosx< m\); \(\forall x\)
\(\Rightarrow\dfrac{m}{\sqrt{\left(2m\right)^2+\left(2m-1\right)^2}}>1\)
\(\Rightarrow m\in\varnothing\)

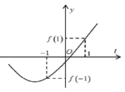
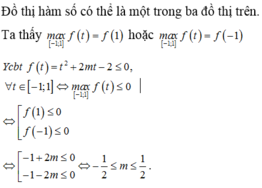
Hàm số xác định trên R khi và chỉ khi:
\(sin^2x+\left(2m-3\right)cosx+3m-2>0;\forall x\in R\)
\(\Leftrightarrow-cos^2x+\left(2m-3\right)cosx+3m-1>0\)
\(\Leftrightarrow t^2-\left(2m-3\right)t-3m+1< 0;\forall t\in\left[-1;1\right]\)
\(\Leftrightarrow t^2+3t+1< m\left(2t+3\right)\)
\(\Leftrightarrow\dfrac{t^2+3t+1}{2t+3}< m\) (do \(2t+3>0;\forall t\in\left[-1;1\right]\))
\(\Leftrightarrow m>\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}\)
Ta có: \(\dfrac{t^2+3t+1}{2t+3}=\dfrac{t^2+t-2+2t+3}{2t+3}=\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}+1\)
Do \(-1\le t\le1\Rightarrow\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}\le0\)
\(\Rightarrow\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}=1\)
\(\Rightarrow m>1\)
Anh giúp em ạ!
https://hoc24.vn/cau-hoi/tim-m-de-ham-so-sqrtsin4xcos4x4sinxcosxm-5-xac-dinh-tren-r.8744969085814