Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Thay x=-2 và y=4 vào (P), ta được:
4a=4
hay a=1
b: Vì (d) đi qua O(0;0) và N(2;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot0+b=0\\2a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=2\end{matrix}\right.\)

a, tự vẽ nha
b, xét pt hđ gđ của P và d ta đc
x2 = x +2
x2 - x - 2= 0
ta có a -b +c=1 +1 -2=0
pt có 2 nghiệm pb x1 = -1 \(\Rightarrow\)y1 = 1
x2 = 2\(\Rightarrow\)y2 = 4
P cắt d tại 2 điểm pb (-1;1) và (2 ;4)
c,A(2;3) \(\in\)d1
thay x=2, y=3 vào d1 ta đc
3= 2a +b (1)
B(-1;2) \(\in\)d1
thay x=-1, y=2 vào d1 ta đc
2 = -a +b (2)
từ 1 và 2 \(\Rightarrow\)hpt \(\hept{\begin{cases}2a+b=3\\-a+b=2\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}3a=1\\-a+b=2\end{cases}}\)\(\hept{\begin{cases}a=\frac{1}{3}\\-\frac{1}{3}+b=2\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}a=\frac{1}{3}\\b=\frac{7}{3}\end{cases}}\)
(d1) y= 1/3x +7/3
#mã mã#
Bạn tham khảo link này nha:
https://olm.vn/hoi-dap/detail/220087948444.html
Chúc bạn học tốt
Forever

a: Thay x=2 và y=1 vào (d), ta được:
2m-2+2=1
hay \(m=\dfrac{1}{2}\)

c: Gọi (d): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Vì (d)//(d1) nên \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b\ne0\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{1}{2}x\)+b
Thay x=4 và y=5 vào (d), ta được:
\(b+\dfrac{1}{2}\cdot4=5\)
=>b+2=5
=>b=3
Vậy: (d): \(y=\dfrac{1}{2}x+3\)

a. pt đường thẳng có dạng: \(y=ax\left(a\ne0\right)\)
Vì (d) đi qua M (2;4) nên thay \(\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\) vào:
\(\Rightarrow4=2a\Leftrightarrow a=2\)
\(\Rightarrow\left(d\right):y=2x\)
b. pt dạng parabol có dạng: \(y=ax^2\left(a\ne0\right)\)
Vì (P) đi qua M (2;4) nên thay \(\left\{{}\begin{matrix}x=2\\y=4\end{matrix}\right.\) vào:
\(\Rightarrow4=2^2.a\Leftrightarrow a=1\)
\(\Rightarrow\left(P\right):y=x^2\)
Vẽ thì bạn tự vẽ nha :)
Tọa độ giao điểm của (P) và (d) là nghiệm của hpt:
\(hpt:\left\{{}\begin{matrix}y=x^2\\y=2x\end{matrix}\right.\Rightarrow pt:x^2=2x\Leftrightarrow x^2-2x=0\) (*)
Xét pt (*) ta có: \(\Delta=\left(-2\right)^2-4.1.0=4>0\)
\(\Rightarrow pt\) có 2 nghiệm phân biệt
\(\Rightarrow\left\{{}\begin{matrix}x_1=\frac{2+\sqrt{4}}{2}=2\\x_2=\frac{2-\sqrt{4}}{2}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y_1=4\\y_2=0\end{matrix}\right.\)
Vậy (P) và (d) có 2 điểm chung và tọa độ của chúng lần lượt là \(\left(2;4\right)\) và \(\left(0;0\right)\)
( Mới học k biết đúng k :))))

a. Em tự giải
b. Từ giả thiết ta có \(A\left(-2;1\right)\) và \(B\left(4;4\right)\)
Gọi phương trình (d) có dạng \(y=ax+b\), do (d) qua A và B nên:
\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x+2\)
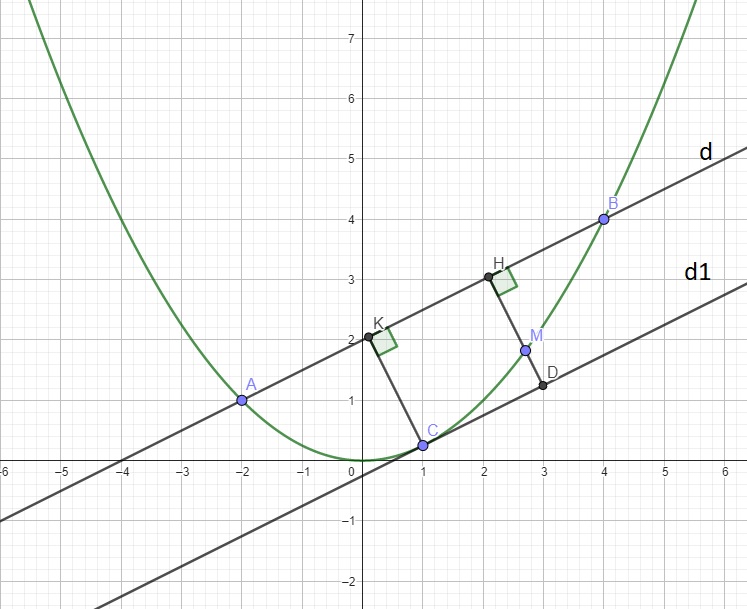
c. Câu này có vài cách giải cho lớp 9, cách nhanh nhất là sử dụng tính chất tiếp tuyến.
Từ M kẻ \(MH\perp AB\Rightarrow S_{ABM}=\dfrac{1}{2}MH.AB\)
Do AB cố định \(\Rightarrow S_{max}\) khi \(MH_{max}\)
Gọi \(d_1\) là đường thẳng song song d và tiếp xúc (P), gọi C là tiếp điểm \(d_1\) và (P)
Do \(d_1\) song song (d) nên pt có dạng: \(y=\dfrac{1}{2}x+b\)
Phương trình hoành độ giao điểm \(d_1\) và (P):
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+b\Rightarrow x^2-2x-4b=0\) (1)
Do \(d_1\) tiếp xúc (P) \(\Rightarrow\left(1\right)\) có nghiệm kép
\(\Rightarrow\Delta'=1+4b=0\Rightarrow b=-\dfrac{1}{4}\)
Thế vào (1) \(\Rightarrow x_C^2-2x_C+1=0\Rightarrow x_C=1\Rightarrow y_C=\dfrac{1}{4}\) \(\Rightarrow C\left(1;\dfrac{1}{4}\right)\)
Từ C kẻ \(CK\perp d\)
Giả sử HM kéo dài cắt \(d_1\) tại D \(\Rightarrow\) tứ giác CKHD là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông)
\(\Rightarrow CK=DH\)
Mà \(DH=MH+MD\ge MH\Rightarrow CK\ge MH\)
\(\Rightarrow MH_{max}=CK\) khi M trùng C
Hay \(M\left(1;\dfrac{1}{4}\right)\)
a) Để (P) đi qua M(-2;4) thì
Thay x=-2 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot\left(-2\right)^2=4\)
\(\Leftrightarrow a\cdot4=4\)
hay a=1
Vậy: Để (P) đi qua M(-2;4) thì a=1
Còn í b c