Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bảng giá trị:

Đồ thị:
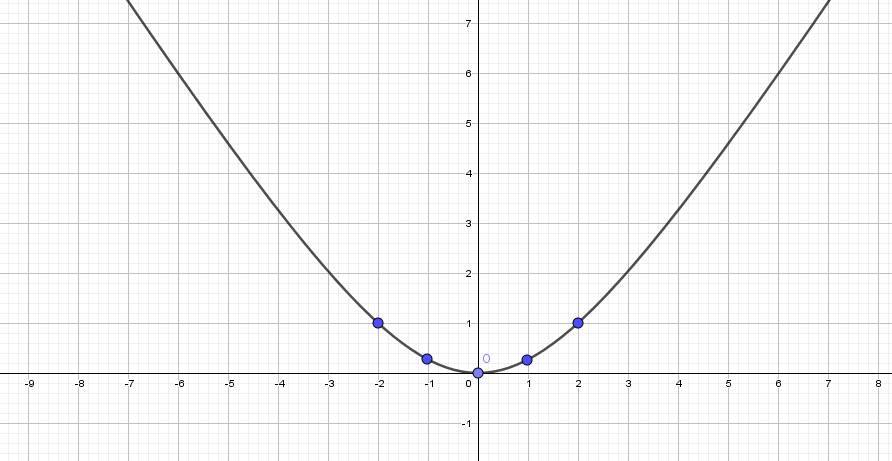
b) Thay y = 100 vào (P) ta được:
\(\dfrac{1}{4}x^2=100\)
\(\Leftrightarrow x^2=100:\dfrac{1}{4}\)
\(\Leftrightarrow x^2=400\)
\(\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-20\end{matrix}\right.\)
Vậy M(-20; 100) hoặc M(20; 100)

Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)

a)Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
\(\Rightarrow2=\left(m-2\right).0+m\) \(\Leftrightarrow m=2\)
Vậy m=2 thì đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3
\(\Rightarrow0=\left(m-2\right)\left(-3\right)+m\) \(\Leftrightarrow m=3\)
Vậy...
c) Hàm số đi qua điểm A(1;2)
\(\Rightarrow2=\left(m-2\right).1+m\)\(\Leftrightarrow m=2\)
Vậy...
a) Đồ thị cắt trục tung tại điểm có tung độ bằng 2
\(\Rightarrow\) điểm đó có tọa độ là \(\left(0;2\right)\)
\(\Rightarrow2=m\)
b) Đồ thị cắt trục hoành tại điểm có hoành độ bằng -3
\(\Rightarrow\) điểm đó có tọa độ là \(\left(-3;0\right)\)
\(\Rightarrow0=-3m+6+m=-2m+6\Rightarrow m=3\)
c) Đồ thị đi qua điểm \(A\left(1;2\right)\)
\(\Rightarrow2=m-2+m\Rightarrow m=2\)

Trước hết xin nói ngay rằng đồ thị của hàm số y = (2x - 1)(x - 1) là một parabol, không có đường tiệm cận nào cả.
Có lẽ bạn muốn nói đến hàm số y = (2x - 1)/(x - 1).
Nếu đúng vậy thì đồ thị của hàm số là một hyperbol vuông góc có hai đường tiệm cận là đường thẳng x = 1 và đường thẳng y = 2.
Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
2, Giao điểm của hai đường tiệm cận là I(1; 2).
Gọi M(x,y) là một điểm trên đồ thị. Hệ số góc của đường thẳng IM là
m = (y - 2)/(x - 1) = {[(2x - 1)/(x - 1)] - 2}/(x - 1) = [(2x - 1) - 2(x - 1)]/(x - 1)²
m = 1/(x - 1)²
Hệ số góc của đường tiếp tuyến Mt với đồ thị tại M(x,y) là
m' = dy/dx = -1/(x - 1)²
Muốn cho MI và Mt thẳng góc với nhau thì điều kiện cần và đủ là
mm' = -1
-1/(x - 1)^4 = -1
(x - 1)^4 = 1
(x - 1)² = 1
x - 1 = ±1
x = 0 hay x = 2
Có 2 điểm M thỏa mãn điều kiện của bài toán là (0; 1) và (2; 3)
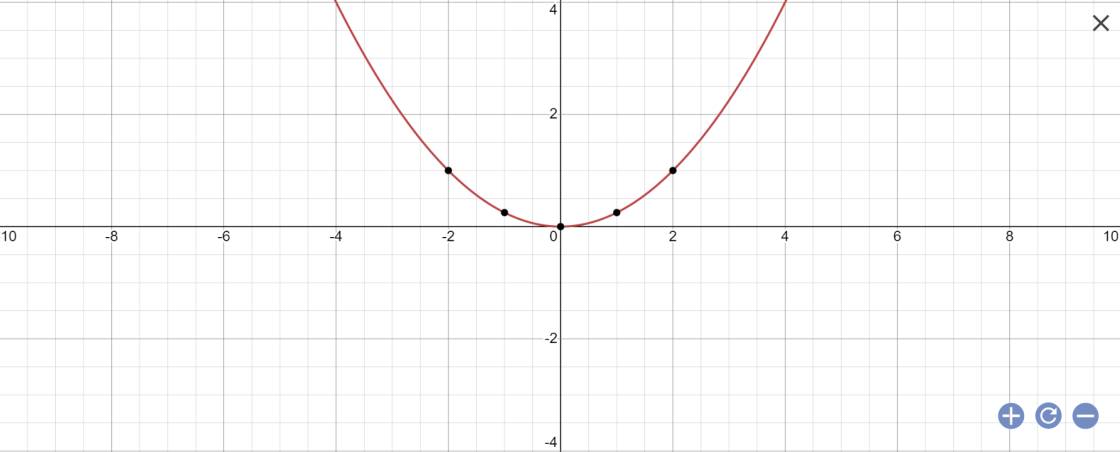
Do tung độ của M bằng 25 nên hoành độ M thỏa mãn:
\(25=\dfrac{1}{4}x^2\Leftrightarrow x^2=100\Rightarrow\left[{}\begin{matrix}x=10\\x=-10\end{matrix}\right.\)
Dạ em cản ơn