Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pt hoành độ giao điểm của đồ thị hàm số (C) với đường thẳng d là:
\(\dfrac{x-1}{x+1}=m-x\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\g\left(x\right)=x^2+\left(2-m\right)x-m-1=0\left(1\right)\end{matrix}\right.\)
Đồ thị (C) cắt đường thẳng d tại 2 điểm phân biệt <=> pt(1) có 2 nghiệm phân biệt khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\g\left(-1\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2+8>0\\-2\ne0\end{matrix}\right.\)
Khi đó: \(x_A,x_B\) là nghiệm của pt (1). Vì tiếp tuyến tại A và B //
\(\Rightarrow f'\left(x_A\right)=f'\left(x_B\right)\Leftrightarrow\dfrac{2}{\left(x_A+1\right)^2}=\dfrac{2}{\left(x_B+1\right)^2}\Leftrightarrow\left[{}\begin{matrix}x_A=x_B\left(loai\right)\\x_A+x_B=-2\end{matrix}\right.\)
Theo định lí Viet ta có:
\(x_A+x_B=m-2\Rightarrow m-2=-2\Leftrightarrow m=0\)

\(\left(m^2-3m-5\right)x-y-2m+19=0\)
\(\Leftrightarrow y=\left(m^2-3m-5\right)x-2m+19\)
Ta có:
\(f'\left(x\right)=-3x^2+4x-1\)
\(f'\left(2\right)=-5\)
Phương trình tiếp tuyến tại A:
\(y=-5\left(x-2\right)+3\Leftrightarrow y=-5x+13\)
Để hai đường thẳng song song:
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m-5=-5\\-2m+19\ne13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m=0\\2m\ne6\end{matrix}\right.\)
\(\Leftrightarrow m=0\)

\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
a. \(\dfrac{2x+2}{x-1}=-2\Rightarrow2x+2=-2x+2\Rightarrow x=0\Rightarrow y'\left(0\right)=-4\)
Phương trình tiếp tuyến: \(y=-4\left(x-0\right)-2\)
b. Tiếp tuyến song song đường thẳng đã cho nên có hệ số góc k=-4
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-2\\x=2\Rightarrow y=6\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4\left(x-0\right)-2\\y=-4\left(x-2\right)+6\end{matrix}\right.\)
c. Gọi \(M\left(x_0;y_0\right)\) là tọa độ tiếp điểm
Pt tiếp tuyến qua M có dạng: \(y=\dfrac{-4}{\left(x_0-1\right)^2}\left(x-x_0\right)+\dfrac{2x_0+2}{x_0-1}\)
Do tiếp tuyến qua A nên:
\(3=\dfrac{-4}{\left(x_0-1\right)^2}\left(4-x_0\right)+\dfrac{2x_0+2}{x_0-1}\)
\(\Leftrightarrow x_0^2-10x_0+21=0\Rightarrow\left[{}\begin{matrix}x_0=3\Rightarrow y'\left(3\right)=-1;y\left(3\right)=4\\x_0=7;y'\left(7\right)=-\dfrac{1}{9};y\left(7\right)=\dfrac{8}{3}\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-1\left(x-3\right)+4\\y=-\dfrac{1}{9}\left(x-7\right)+\dfrac{8}{3}\end{matrix}\right.\)
d.
Do tiếp tuyến tạo với 2 trục tọa độ 1 tam giác vuông cân nên có hệ số góc bằng 1 hoặc -1
\(\Rightarrow\left[{}\begin{matrix}\dfrac{-4}{\left(x-1\right)^2}=1\left(vô-nghiệm\right)\\\dfrac{-4}{\left(x-1\right)^2}=-1\end{matrix}\right.\)
\(\Rightarrow\left(x-1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=3\Rightarrow y=4\\x=-1\Rightarrow y=0\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn:
\(\left[{}\begin{matrix}y=-1\left(x-3\right)+4\\y=-1\left(x+1\right)+0\end{matrix}\right.\)

- Hàm số đã cho xác định với ∀x ∈ R.
- ta có:
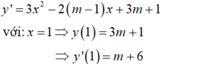
- Phương trình tiếp tuyến tại điểm có hoành độ x = 1 là:
y = (m+ 6)(x – 1) + 3m + 1
- Tiếp tuyến này đi qua A(2; - 1) nên có:
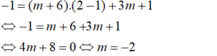
- Vậy m = -2 là giá trị cần tìm.

\(y'=\dfrac{-3}{\left(x-1\right)^2}\)
Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\dfrac{-3}{\left(x_0-1\right)^2}\left(x-x_0\right)+\dfrac{2x_0+1}{x_0-1}\) (1)
a.
Tọa độ A và B có dạng: \(A\left(\dfrac{2x_0^2+2x_0-1}{3};0\right)\) ; \(B\left(0;\dfrac{2x_0^2+2x_0-1}{\left(x_0-1\right)^2}\right)\)
\(\Rightarrow OA=\left|\dfrac{2x_0^2+2x_0-1}{3}\right|;OB=\dfrac{\left|2x_0^2+2x_0-1\right|}{\left(x_0-1\right)^2}\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{6}\Rightarrow OA.OB=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{\left(2x_0^2+2x_0-1\right)^2}{3\left(x_0-1\right)^2}=\dfrac{1}{3}\Rightarrow\left(2x_0^2+2x_0-1\right)^2=\left(x_0-1\right)^2\)
\(\Leftrightarrow\left(2x_0^2+3x_0-2\right)\left(2x_0^2+x_0\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x_0=0\\x_0=-\dfrac{1}{2}\\x_0=-2\\x_0=\dfrac{1}{2}\end{matrix}\right.\)
Có 4 tiếp tuyến thỏa mãn:... (thế lần lượt các giá trị \(x_0\) vào (1) là được)
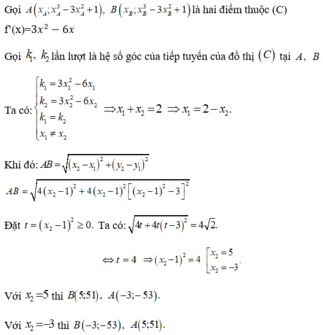
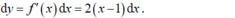
Gọi điểm cố định có tọa độ \(x_0;y_0\Rightarrow\) với mọi M ta có:
\(x_0^4-y_0+1-m\left(x_0^2-4\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0^2-4=0\\x_0^4-y_0+1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}A\left(2;17\right)\\B\left(-2;17\right)\end{matrix}\right.\)
\(y'=4x^3-2mx\) \(\Rightarrow\left\{{}\begin{matrix}y'\left(2\right)=32-4m\\y'\left(-2\right)=-32+4m\end{matrix}\right.\)
Tiếp tuyến tại A: \(y=\left(32-4m\right)\left(x-2\right)+17=\left(32-4m\right)x+8m-47\)
Tiếp tuyến tại B: \(y=\left(4m-32\right)\left(x+2\right)+17=\left(4m-32\right)x+8m-47\)
Hai tiếp tuyến song song khi: \(\left\{{}\begin{matrix}32-4m=4m-32\\8m-17\ne8m-17\end{matrix}\right.\)
Không tồn tại m thỏa mãn