Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Làm lại: phân tích nhân tử nhầm:
1) để y đi qua A(1,0) \(\Leftrightarrow1-\left(m+1\right)+\left(m-1\right)+1=0=0+0+0=0\Rightarrow dung..\forall m\)2) y(x)=\(x^2\left(x-1\right)-mx\left(x-1\right)-\left(x-1\right)=\left(x-1\right)\left(x^2-mx-1\right)\)
x^3-mx^2-x-x^2+mx+1=x^3-(m+1)x^2+(m-1)x+1 {không sai được nữa}
2)Để y cắt Ox tại hai điểm B,C cần
\(\left\{\begin{matrix}1-m-1\ne0\\x^2-mx-1=0co.2N_o\end{matrix}\right.\)
\(\Leftrightarrow\left\{\begin{matrix}m\ne0\\\Delta=m^2+4>0\end{matrix}\right.\) \(\Rightarrow m\ne0\)
\(\left\{\begin{matrix}x_b=\dfrac{m-\sqrt{m^2+4}}{2}\\x_c=\dfrac{m+\sqrt{m^2+4}}{2}\end{matrix}\right.\)
\(y'\left(x\right)=3x^2-2\left(m+1\right)x+\left(m-1\right)\)
GIAO luu;
\(y=\left(x-1\right)\left(x^2+x+1\right)-m\left(x^2-x\right)+\left(x^2-x\right)\)
m cần thỏa mãn 3 điều kiện
(1) y đi qua A; (2) có 3 nghiệm (3) tiếp tuyến //
Thỏa mãn ĐK(1)
\(y=\left(x-1\right)\left[x^2-\left(m-2\right)x+1\right]\)=>\(x=1\Rightarrow y=0\forall m\Rightarrow\) y luôn đi qua A(1;0)
kết luận (1) Đúng mọi m.(*)
Thỏa mãn ĐK (2)
Để y cắt Ox tại B,C phân biệt:
cần: \(\left\{\begin{matrix}x^2-\left(m-2\right)x+1=0\left(1\right)có.2N_0\\1-\left(m-2\right)+1\ne0\Rightarrow m\ne4\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\Delta_x>0\Rightarrow m^2-4m>0\Rightarrow\left[\begin{matrix}m< 0\\m>4\end{matrix}\right.\)
kết luận (2) \(\left\{\begin{matrix}m\ne4\\\left[\begin{matrix}m< 0\\m>4\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[\begin{matrix}m< 0\\m>4\end{matrix}\right.\)(**)
Thỏa mãn ĐK (3)
\(y'=3x^2-2\left(m+1\right)x+\left(m-1\right)\)
Để Tiếp tuyến tại B//C cần: \(y'\left(x_b\right)=y'\left(x_c\right)\)
Thay \(x_b\&x_c\Rightarrow g\left(m\right)=0\Rightarrow m\)
p/s: "Hiểu thế nào làm thế đó, chưa biết đúng hay sai.Ai đi qua test hộ cái"
Điều kiện: \(x\ne1\)
a) Xét phương trình: \(\frac{x^2-2mx+3m-2}{x-1}=0\Leftrightarrow x^2-2mx+3m-2=0\)\(\left(x-1\ne0\right)\)
Pt có hai nghiệm phân biệt \(\Leftrightarrow\Delta'>0\Leftrightarrow m^2-3m+2>0\Leftrightarrow\orbr{\begin{cases}m>2\\m< 1\end{cases}}\)
Khi đó \(\hept{\begin{cases}x_1=m-\sqrt{m^2-3m+2}\\x_2=m+\sqrt{m^2-3m+2}\end{cases}}\)
+) \(x_1,x_2\ne1\Leftrightarrow\hept{\begin{cases}m-\sqrt{m^2-3m+2}\ne1\\m+\sqrt{m^2-3m+2}\ne1\end{cases}\Leftrightarrow m\ne1}\)
+) Tiếp tuyến của đồ thị tại hai giao điểm với trục Ox vuông góc với nhau
\(\Leftrightarrow\hept{\begin{cases}y'\left(x_1\right)=-1\left(1\right)\\y'\left(x_2\right)=1\left(2\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow\frac{\left(2x_1-2m\right)\left(x_1-1\right)-\left(x_1^2-2mx_1+3m-2\right)}{\left(x_1-1\right)^2}=-1\)
\(\Leftrightarrow\frac{m-1}{\left(x_1-1\right)^2}=2\Rightarrow m-1=2\left(m-\sqrt{m^2-3m+2}-1\right)^2\)
\(\Leftrightarrow\left(m-1\right)\left[1-2\left(2m-3-2\sqrt{m^2-3m+2}\right)\right]=0\)
\(\Leftrightarrow4\sqrt{m^2-3m+2}=4m-7\Leftrightarrow\hept{\begin{cases}m\ge\frac{7}{4}\\m=\frac{17}{8}\end{cases}}\Leftrightarrow m=\frac{17}{8}\)(t/m m>2 v m<1)
Giải (2) cho ra \(m=1\)(loại). Vậy m cần tìm là \(m=\frac{17}{8}.\)
- Ta có : (d) : 2x – y – 3 = 0 ⇔ y = 2x - 3. Đường thẳng d có hệ số góc kd = 2 .
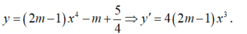
- Hệ số góc của tiếp tuyến của đồ thị hàm số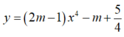 
tại điểm có hoành độ x = -1 là:
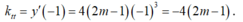
- Do tiếp tuyến vuông góc với đường thẳng d nên ta có:
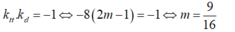
Chọn D.
x^2+(y-1)^2=4
=>R=2 và I(0;1)
A(1;1-m) thuộc (C)
y'=4x^3-4mx
=>y'(1)=4-4m
PT Δsẽ là y=(4-m)(x-1)+1-m
Δ luôn đi qua F(3/4;0) và điểm F nằm trong (λ)
Giả sử (Δ) cắt (λ) tại M,N
\(MN=2\sqrt{R^2-d^2\left(I;\Delta\right)}=2\sqrt{4-d^2\left(I;\Delta\right)}\)
MN min khi d(I;(Δ)) max
=>d(I;(Δ))=IF
=>Δ vuông góc IF
Khi đó, Δ có 1 vecto chỉ phương là: vecto u vuông góc với vecto IF=(3/4;p-1)
=>vecto u=(1;4-4m)
=>1*3/4-(4-4m)=0
=>m=13/16
\(y'=4x^3-4mx\Rightarrow y'\left(1\right)=4-4m\)
\(A\left(1;1-m\right)\)
Phương trình tiếp tuyến d tại A có dạng:
\(y=\left(4-4m\right)\left(x-1\right)+1-m\)
\(\Leftrightarrow\left(4-4m\right)x-y+3m-3=0\)
\(d\left(B;d\right)=\dfrac{\left|\dfrac{3}{4}\left(4-4m\right)-1+3m-3\right|}{\sqrt{\left(4-4m\right)^2+1}}=\dfrac{1}{\sqrt{\left(4-4m\right)^2+1}}\le1\)
Dấu "=" xảy ra khi và chỉ khi \(4-4m=0\Rightarrow m=1\)
y′=4x3−4mx⇒y′(1)=4−4my′=4x3−4mx⇒y′(1)=4−4m
A(1;1−m)A(1;1−m)
Phương trình tiếp tuyến d tại A có dạng:
y=(4−4m)(x−1)+1−my=(4−4m)(x−1)+1−m
⇔(4−4m)x−y+3m−3=0⇔(4−4m)x−y+3m−3=0
d(B;d)=∣∣∣34(4−4m)−1+3m−3∣∣∣√(4−4m)2+1=1√(4−4m)2+1≤1d(B;d)=|34(4−4m)−1+3m−3|(4−4m)2+1=1(4−4m)2+1≤1
Dấu "=" xảy ra khi và chỉ khi 4−4m=0⇒m=1
\(y'=8x^3-8x\)
a. Đường thẳng \(x-48y+1=0\) có hệ số góc \(\dfrac{1}{48}\) nên tiếp tuyến có hệ số góc \(k=-48\)
\(\Rightarrow8x^3-8x=-48\Rightarrow x^3-x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+3\right)=0\Rightarrow x=-2\)
\(y'\left(-2\right)=47\)
Phương trình tiếp tuyến: \(y=-48\left(x+2\right)+47\)
b. Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\left(8x_0^3-8x_0\right)\left(x-x_0\right)+2x^4_0-4x^2_0-1\) (1)
Do tiếp tuyến qua A:
\(\Rightarrow-3=\left(8x_0^3-8x_0\right)\left(1-x_0\right)+2x_0^4-4x^2_0-1\)
\(\Leftrightarrow3x_0^4-4x_0^3-2x_0^2+4x_0-1=0\)
\(\Leftrightarrow\left(x_0-1\right)^2\left(3x_0^2+2x_0-1\right)=0\Rightarrow\left[{}\begin{matrix}x_0=1\\x_0=-1\\x_0=\dfrac{1}{3}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn. Thay lần lượt các giá trị \(x_0\) bên trên vào (1) là được
