Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có
4
m
3
+
m
2
f
2
x
+
5
=
f
2
x
+
3
Xét hàm 
và đi đến kết quả 
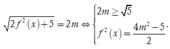
Ta có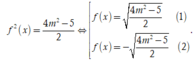 
Với điều kiện 
thì phương trình (2) luôn có một nghiệm duy nhất, để phương trình đã cho có 3 nghiệm phân biệt
⇔
(1) có 2 nghiệm phân biệt khác nghiệm của phương trình (2)
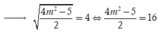
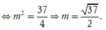
Chọn B.
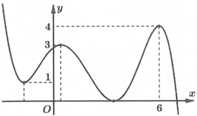
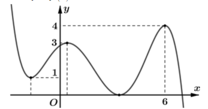
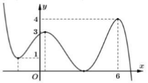
Để phương trình f(cosx) = m có 3 nghiệm x phân biệt thuộc khoảng ( 0 ; 3 π 2 ] thì phương trình f(cosx) = m phải có hai nghiệm cosx phân biệt, trong đó có 1 nghiệm thuộc (-1;0] và một nghiệm thuộc (0;1)
Dựa vào đồ thị, suy ra m ∈ (0;2)
Chọn B.
Chọn đáp án B
Phương pháp
+) Đặt t=cosx, xác định khoảng giá trị của t, khi đó phương trình trở thành f(t)=m.
+) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và y=m song song với trục hoành.
Cách giải
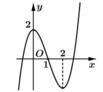
Đặt t=cosx ta có
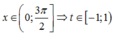
Khi đó phương trình trở thành f(t)=m.
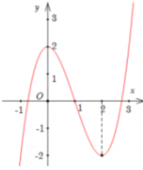
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(t) và y=m song song với trục hoành.
Dựa vào đồ thị hàm số y=f(x) ta thấy phương trình f(t)=m có 2 nghiệm phân biệt thuộc [-1;1) khi và chỉ khi mÎ(0;2).
Có 
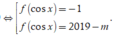
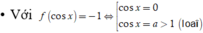
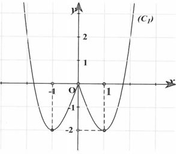
Phương trình này có hai nghiệm 
• Với 
ta cần tìm điều kiện để phương trình này có 4 nghiệm phân biệt thuộc 
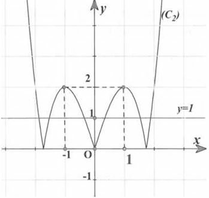
Với t = -1 phương trình (1) cho đúng một nghiệm x =
π
; với t = 0 phương trình cho hai nghiệm 
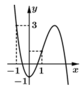
Với mỗi 
phương trình cho hai nghiệm thuộc
Vậy điều kiện cần tìm là phương trình (1) phải có hai nghiệm phân biệt
Chọn B.
Đáp án C
Với f x > 0 , ∀ x ∈ ℝ . Xét biểu thức f ' x f x = 2 - 2 x *
Lấy nguyên hàm 2 vế (*), ta được ∫ d f x f x = ∫ 2 - 2 x d x
⇔ ∫ d f x f x = - x 2 + 2 x + C ⇔ ln f x = - x 2 + 2 x + C
Mà f(0) =1 suy ra C = lnf(0) = ln1 = 0. Do đó f x = e - x 2 + 2 x
Xét hàm số f x = e - x 2 + 2 x trên - ∞ ; + ∞ , có f ' x = - 2 x + 2 = 0 ⇔ x = 1
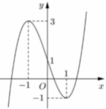
Tính giá trị f 1 = e ; lim x → - ∞ f x = 0 ; lim x → - ∞ f x = 0
Suy ra để phương trình f(x) = m có hai nghiệm thực phân biệt ⇔ 0 < m < e .
Chọn đáp án B.