Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
có 3 điểm cực trị.
Chọn D
Xét hàm số 
.
Có 
.
Ta lại có 
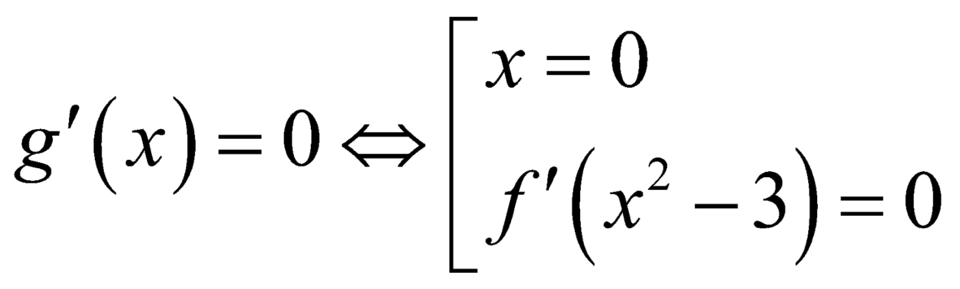
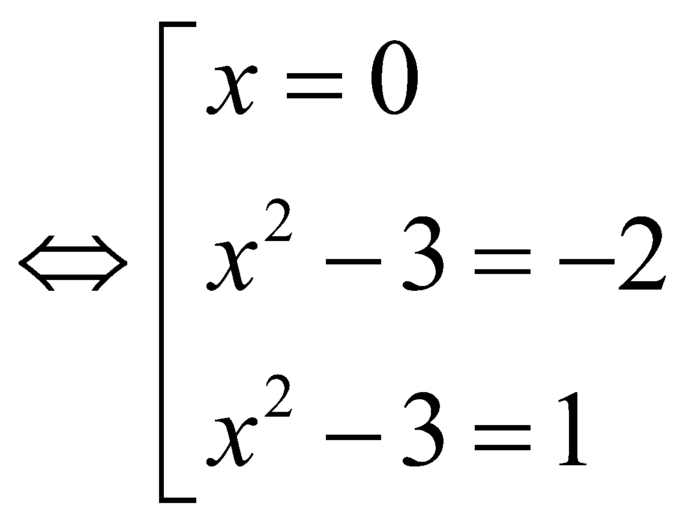
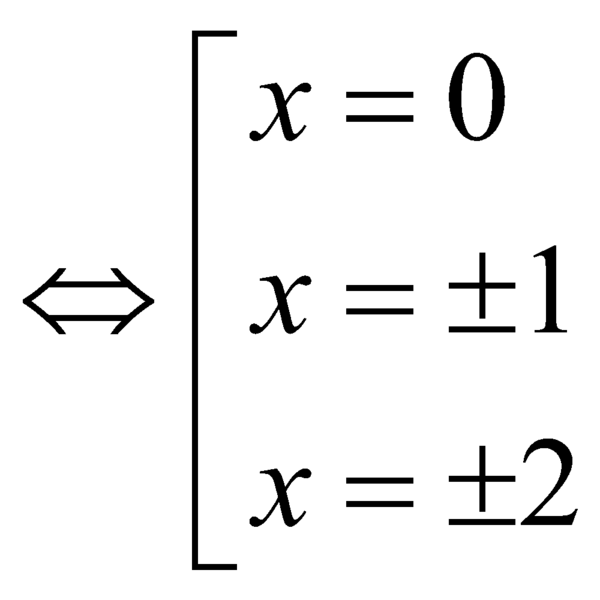thì 
. Do đó 
thì 
.
thì 
. Do đó 
thì 
.
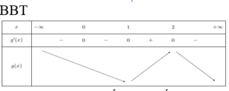
Từ đó ta có bảng biến thiên của 
như sau
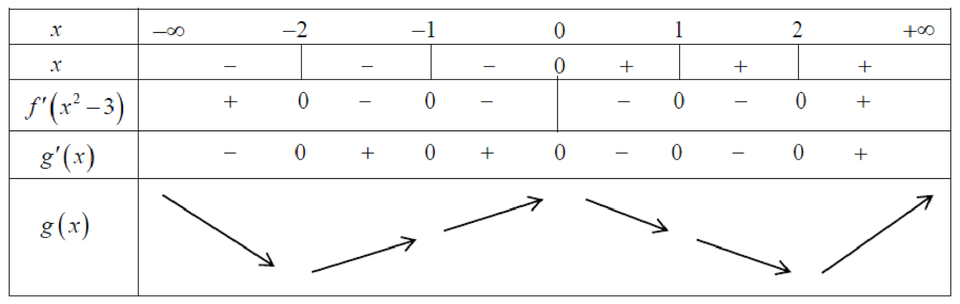
Dựa vào bảng biến thiên, ta có
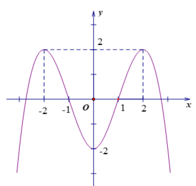
I. Hàm số 
có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
II. Hàm số 
đạt cực tiểu tại 
LÀ MỆNH ĐỀ SAI.
III. Hàm số 
đạt cực đại tại 
LÀ MỆNH ĐỀ SAI.
IV. Hàm số 
đồng biến trên khoảng 
LÀ MỆNH ĐỀ ĐÚNG.
V. Hàm số 
nghịch biến trên khoảng 
LÀ MỆNH ĐỀ SAI.
Vậy có hai mệnh đề đúng.
ở chỗ x<1=> x= -2 thì sao bạn ơi =>(x^2 -3) =1 >0 thì sao f ' (...)>0 được ????
a.
TXĐ: \(D=\left[-4;2\right]\)
\(0\le\sqrt{9-\left(x+1\right)^2}\le3\Rightarrow-1\le\sqrt{9-\left(x+1\right)^2}\le2\)
\(\Rightarrow f'\left(\sqrt{8-x^2-2x}-1\right)\le0\) ; \(\forall x\in D\)
\(g'\left(x\right)=-\dfrac{x+1}{\sqrt{8-x^2-2x}}.f'\left(\sqrt{8-x^2-2x}-1\right)\) luôn cùng dấu \(x+1\)
\(\Rightarrow g\left(x\right)\) đồng biến trên \(\left[-1;2\right]\) và nghịch biến trên \(\left[-4;-1\right]\)
Từ BBT ta thấy \(g\left(x\right)_{max}=g\left(-4\right)=g\left(2\right)=f\left(-1\right)=?\)
\(g\left(x\right)_{min}=g\left(-1\right)=f\left(2\right)=?\)
(Do đề chỉ có thế này nên ko thể xác định cụ thể được min-max)
b.
\(g'\left(x\right)=\left(2x+1\right).f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\f'\left(x^2+x\right)=0\left(1\right)\end{matrix}\right.\)
Xét (1), ta chỉ cần quan tâm 2 nghiệm bội lẻ:
\(f'\left(x^2+x\right)=0\Rightarrow\left[{}\begin{matrix}x^2+x=-1\left(vô-nghiệm\right)\\x^2+x=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\) \(\Rightarrow x^2+x\ge2\) ; với \(-2\le x\le1\Rightarrow-1\le x^2+x\le2\) nên ta có bảng xét dấu:
Từ BBT ta có: \(x=-\dfrac{1}{2}\) là cực đại, \(x=-2;x=1\) là 2 cực tiểu
Hàm đồng biến trên ... bạn tự kết luận
Chọn C.
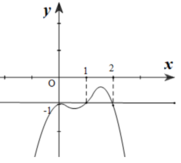
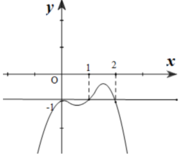
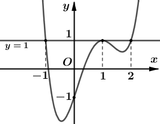
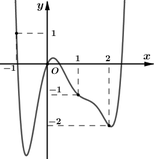
Vì đề bài hỏi điểm cực tiểu của đồ thị hàm số, dựa hình vẽ ta thấy điểm 
là điểm cực tiểu của đồ thị hàm số.
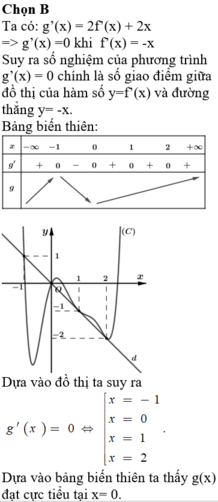
Chọn B
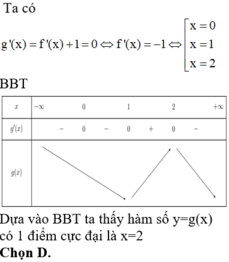
Ta có g’(x) = f’(x) + 1.
Đồ thị của hàm số y= g’(x) là phép tịnh tiến đồ thị của hàm số y= f’(x) theo phương song song với Oy lên trên 1 đơn vị.
Khi đó đồ thị hàm số y= g’(x) cắt trục hoành tại hai điểm phân biệt.
=> Hàm số y= g(x) có 2 điểm cực trị.
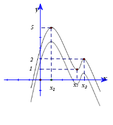
Ta có 
Suy ra đồ thị của hàm số g’ (x) là phép tịnh tiến đồ thị hàm số y= f’ (x) theo phương Oy xuống dưới 
đơn vị.
Ta có 
và dựa vào đồ thị của hàm số y= f’ (x), ta suy ra đồ thị của hàm số g’ (x) cắt trục hoành tại 4 điểm.
Chọn D.
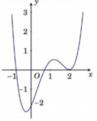
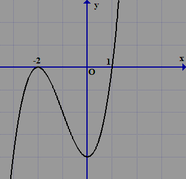
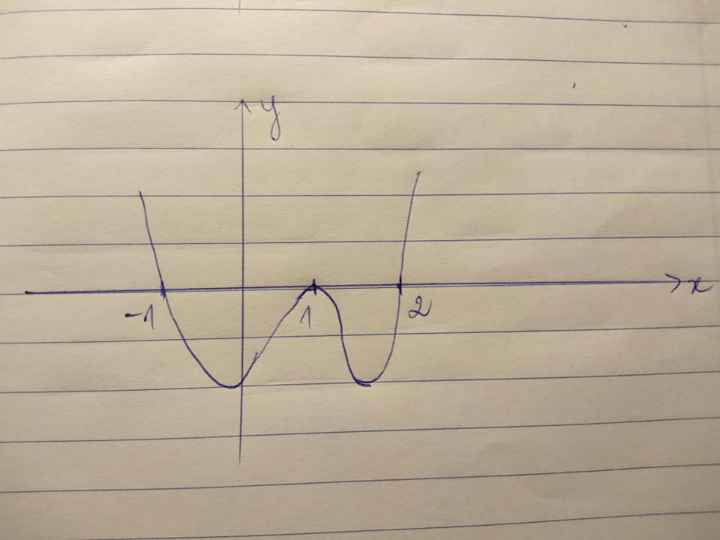
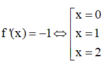
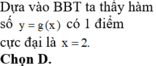
Chọn B
Số nghiệm của phương trình (*) là số giao điểm của đồ thị y = f ' x
và đường thẳng d : y = x - 1
Phương trình (*) có 4 nghiệm đơn
nên hàm số g x có 2 điểm cực tiểu, 2 điểm cực đại