Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.


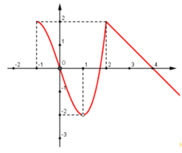
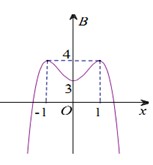
Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B

Đáp án B
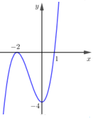
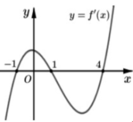
Dựa vào đồ thị hàm số f ' ( x ) ta thấy f ' ( x ) đổi dấu từ âm sang dương khi qua điểm x = 1 nên x = 1 là điểm cực tiểu của hàm số f ( x )
f ' ( x ) không đổi dấu khi đi qua điểm x = -2 nên x = -2 không phải điểm cực trị

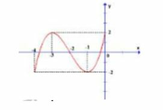
Ta có f ' ( x ) = 0 ⇔ x = - 1 ; x = 1 ; x = 4 và f '(x) đổi dấu từ dương qua âm khi qua điểm x = 1. Vậy hàm số y=f(x) đạt cực đại tại điểm x = 1.
Chọn đáp án C.





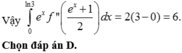
Đáp án B
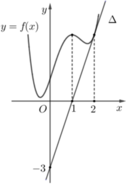
Dựa vào đồ thị hàm số f ' ( x ) ta thấy f ' ( x ) đổi dấu từ âm sang dương khi qua điểm x = 1 nên x = 1 là điểm cực tiểu của hàm số f ( x )
f ' ( x ) không đổi dấu khi đi qua điểm x = -2 nên x = -2 không phải điểm cực trị