

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C.
Ta có:
g x = x . f 2 x − 1 ⇒ g ' x = f 2 x − 1 + 2 x . f ' 2 x − 1
Suy ra g ' 1 = f 1 + 2 f ' 1 mà d 1 vuông góc với d 2 ⇒ f ' 1 . g ' 1 = − 1
⇔ f ' 1 . f 1 + 2 f ' 1 = − 1 ⇔ 2. f ' 1 2 + f 1 + 1 = 0 ( * )
Phương trình (*) có nghiệm khi và chỉ khi:
Δ = f 1 2 − 4.2 ≥ 0 ⇔ f 1 ≥ 2 2 .

Chọn C.
Dựa vào đồ thị hàm số f ' ( x ) suy ra BBT của hàm số y = f(x)

Khẳng định 1, 2, 5 đúng, khẳng định 4 sai.
Xét khẳng định 3: Ta có:
f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) ⇒ f ( 3 ) - f ( 0 ) = f ( 1 ) - f ( 2 ) > 0
Do đó f ( 3 ) > f ( 0 ) ⇒ Vậy khẳng định 3 đúng.

Chọn đáp án C
Ta có
![]()
Đường thẳng d 1 là tiếp tuyến của đồ thị hàm số y = f x tại điểm x = 1 nên có hệ số góc là k 1 = f ' 1
Đường thẳng d 2 là tiếp tuyến của đồ thị hàm y = g x = x . f 2 x - 1 tại điểm x = 1 nên có hệ số góc là
k 2 = g ' 1 = f 1 + 2 f ' 1
Mà d 1 ⊥ d 2 nên
![]()
![]()
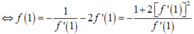
Do f ' 1 ≠ 0 nên
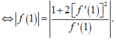
Đặt f ' 1 = t t ≠ 0
Xét hàm số f t = 1 + 2 t 2 t
* Nếu t > 0 thì
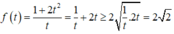
* Nếu t < 0 thì

Vậy h t ≤ 2 2 , ∀ t ≠ 0 hay f 1 ≥ 2 2