Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hàm số:
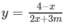
a) TXĐ: R \ {−3m/2}
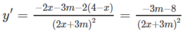
+) Nếu m < −8/3, y′ > 0 suy ra hàm số đồng biến trên các khoảng 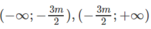
+) Nếu m > −8/3, y′ < 0 suy ra hàm số nghịch biến trên các khoảng
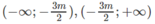
+) Nếu m = −8/3 thì y = −1/2 khi x ≠ 4
b) Ta có:
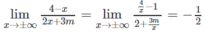
nên với mọi m, đường thẳng y = -1/2 là tiệm cận ngang và đi qua 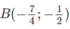
c) Số giao điểm của (Cm) và đường phân giác của góc phần tư thứ nhất là số nghiệm của phương trình:
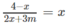
Ta có:
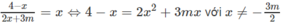
⇔ 2 x 2 + (3m + 1)x – 4 = 0 ⇔ 2 x 2 + (3m + 1) x – 4 = 0 với x ≠ −3m/2
+) Thay x = −3m/2 vào (*), ta có:
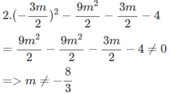
Như vậy, để x = −3m/2 không là nghiệm của phương trình (*) ta phải có m ≠ −8/3.
Ta có: Δ = ( 3 m + 1 ) 2 + 32 > 0, ∀ m. Từ đó suy ra với m ≠−8/3 đường thẳng y = x luôn cắt (Cm) tại hai điểm phân biệt.
d) Ta có:
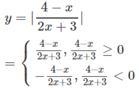
Trước hết, ta vẽ đồ thị (C) của hàm số
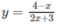
TXĐ: D = R \ {−3/2}.
Vì 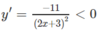
với mọi nên hàm số nghịch biến trên các khoảng
Bảng biến thiên:
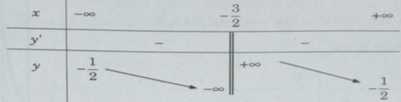
Tiệm cận đứng x = −3/2
Tiệm cận ngang y = −1/2
Đồ thị (C) đi qua các điểm (−2;−6),(−1;5),(0;4/3),(4;0)
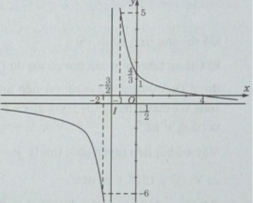
Để vẽ đồ thị (C’) của hàm số , ta giữ nguyên phần đồ thị (C) nằm phía trên trục hoành và lấy đối xứng phần đồ thị (C) nằm phía dưới trục hoành qua trục hoành.
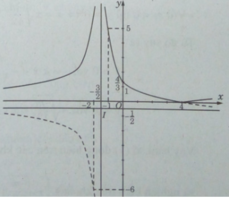

a)
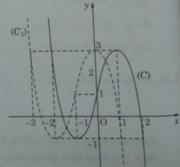
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
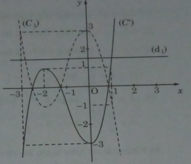
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
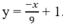
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 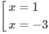
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.

+ Ta có y ' = 3 x + 1 2
+ Gọi M x 0 ; 2 x 0 - 1 x 0 + 1 ∈ C , x 0 ≠ - 1 .
Phương trình tiếp tuyến tại M là
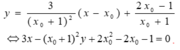
+ 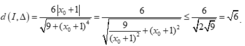
+ Dấu xảy ra khi và chỉ khi
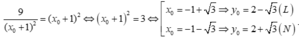
Tung độ này gần với giá trị e nhất trong các đáp án.
Chọn C.

Đáp án A
Gọi ![]() là điểm cố định cần tìm.
là điểm cố định cần tìm.
Ta có ![]()
![]() .
.
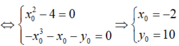
![]()
Lại có
![]()
Phương trình tiếp tuyến của ![]() có dạng
có dạng
![]() hay
hay
![]() .
.
Đường phân giác góc phần tư thứ nhất có phương trình d: y = x.
Vì
∆
vuông góc với d nên ta có ![]() .
.

Phương pháp:
+) Tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
+) Sử dụng công thức tính diện tích tam giác
![]()
+) Sử dụng công thức tính độ dài ![]()
+) Áp dụng định lí Vi-ét tìm m
Chọn C.
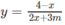
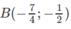
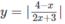



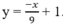
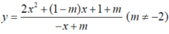 có đồ thị
(
C
m
)
và A là điểm cố định có hoành độ âm của
(
C
m
)
. Giá trị của để tiếp tuyến tại A của
(
C
m
)
vuông góc với đường phân giác góc phần tư thứ nhất là
có đồ thị
(
C
m
)
và A là điểm cố định có hoành độ âm của
(
C
m
)
. Giá trị của để tiếp tuyến tại A của
(
C
m
)
vuông góc với đường phân giác góc phần tư thứ nhất là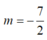
Số giao điểm của ( C m ) và đường phân giác của góc phần tư thứ nhất là số nghiệm của phương trình:
Ta có:
⇔ 2 x 2 + (3m + 1)x – 4 = 0 ⇔ 2 x 2 + (3m + 1) x – 4 = 0 với x ≠ −3m/2
+) Thay x = −3m/2 vào (*), ta có:
Như vậy, để x = −3m/2 không là nghiệm của phương trình (*) ta phải có m ≠ −8/3.
Ta có: ∆ = 3 m + 1 2 + 32 > 0, ∀ m. Từ đó suy ra với m ≠ −8/3 đường thẳng y = x luôn cắt ( C m ) tại hai điểm phân biệt.