Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Đường thẳng đi qua M(1;3) có hệ số góc k có dạng d: y = k(x - 1) + 3.
d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm
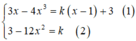
Thay (2) vào (1) ta được
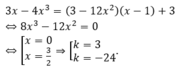
Vậy có 2 tiếp tuyến

y' = 3 - 12x
Đường thẳng (d) có hệ số góc là k đi qua M(1;3) y=k(x-1)+3 .
Đường thẳng (d) tiếp xúc với đồ thì hàm số khi hệ phương trình sau có nghiệm
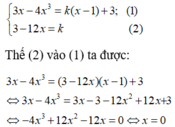
Với x = 0 thì k = 3
Do đó có tối đa hai tiếp tuyến đi qua điểm M(1;3).
Chọn B

+ Giả sử M( x 0 ; y 0 ) ∈ C suy ra y 0 = 2 x 0 + 3 x 0 + 1
+Ta có
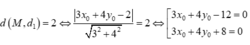
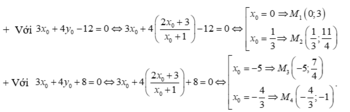
Ta tìm được 4 điểm M suy ra có 4 tiếp tuyến.
Chọn C.

- Giả sử ![]()
- Ta có 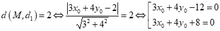
- Với 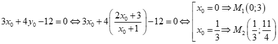
- Với 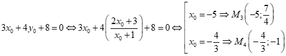
Suy ra có 4 tiếp tuyến.
Chọn C.

+ Xét đường thẳng kẻ từ một điểm bất kì trên đường thẳng x= 2 có dạng:
∆: y= k( x-2) hay y= kx-2k
+ ∆ là tiếp tuyến của (C)
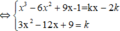
có nghiệm

+ Phương trình bậc ba có duy nhất một nghiệm tương ứng cho ta một giá trị k . Vậy có một tiếp tuyến.
+ Dễ thấy kẻ từ một điểm bất kì trên đường thẳng x=2có dạng y= a song song với trục Ox cũng chỉ kẻ được một tiếp tuyến.
Chọn B.

Đáp án D
Cách giải:
Xét phương trình hoành độ giao điểm của (C) và đường thẳng y = 2x + m:
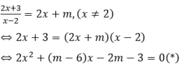
Dễ dàng kiểm tra được x = 2 không phải nghiệm của phương trình (*) với mọi m
Để phương trình (*) có 2 nghiệm phân biệt x1, x2 thì Δ > 0 ⇔ (m - 6)2 + 8(2m + 3) > 0 ⇔ m2 + 4m + 60 > 0, luôn đúng
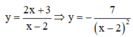
Tiếp tuyến của (C) tại hai điểm giao song song với nhau
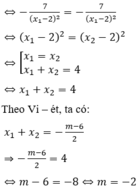
Vậy, có 1 giá trị thực của tham số m thỏa mãn yêu cầu đề bài.

+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.


+ Đường thẳng đi qua M(1;3) có hệ số góc k có dạng d: y=k(x-1)+3 .
+ d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:
Thay (2) vào (1) ta được
Vậy có 2 tiếp tuyến.
Chọn C.