Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ Đạo hàm y’ = 6x2 – 18x+ 12
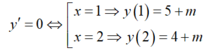
+ Tọa độ hai điểm cực trị của đồ thị hàm số là A( 1; 5+m) và B( 2; 4+ m)
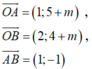
O ; A và B không thẳng hàng nên – 4-m≠ 2 hay m≠ - 6
Chu vi của tam giác OAB là:
![]()

Dấu bằng xảy ra khi và chỉ khi ![]() cùng hướng
cùng hướng 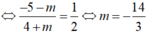 .
.
Vậy chu vi tam giác OAB nhỏ nhất bằng (√10 + √2) khi m= -14/ 3.
Chọn C.

a) Xét hàm số \(y=ax^4+bx^2+c\)
Ta có \(y'=4ax^3+2bx=2x\left(2ax^2+b\right)\)
\(y'=0\Leftrightarrow x=0\) hoặc \(2ax^2+b=0\left(1\right)\)
Đồ thị hàm số có 3 cực trị phân biệt khi và chỉ khi \(y'=0\) có 3 nghiệm phân biệt hay phương trình (1) có 2 nghiệm phân biệt khác 0 \(\Leftrightarrow ab< 0\) (*)
Với điều kiện (*) thì đồ thị có 3 điểm cực trị là :
\(A\left(0;c\right);B\left(-\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right);C\left(\sqrt{-\frac{b}{2a},}c-\frac{b^2}{4a}\right)\)
Ta có \(AB=AC=\sqrt{\frac{b^2-8ab}{16a^2}};BC=\sqrt{-\frac{2b}{a}}\) nên tam giác ABC vuông khi và chỉ khi vuông tại A.
Khi đó \(BC^2=2AB^2\Leftrightarrow b^3+8a=0\)
Do đó yêu cầu bài toán\(\Leftrightarrow\begin{cases}ab< 0\\b^3+8a=0\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\-8\left(m+1\right)^3+8=0\end{cases}\)\(\Leftrightarrow m=0\)
b) Ta có yêu cầu bài toán \(\Leftrightarrow\begin{cases}ab< 0\\OA=BC\end{cases}\)\(\Leftrightarrow\begin{cases}-2\left(m+1\right)< 0\\m^2-4\left(m+1\right)=0\end{cases}\)
\(\Leftrightarrow m=2\pm2\sqrt{2}\)

Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$

`y'=3x^2+4mx=0<=>[(x=0),(x=-4/3m):}` `(m ne 0)`
`=>[(y=-m),(y=32/27 m^3-m):}`
`=>A(0;-m),B(-4/3m;32/27 m^3-m)`
Để `\triangle OAB` vuong tại `O`
`=>\vec{OA}.\vec{OB}=0`
`<=>(0;-m).(-4/3m;32/27 m^3 -m)=0`
`<=>0.(-4/3m)-m(32/27 m^3-m)=0`
`<=>m^2(32/27m^2 -1)=0`
`<=>[(m=0(L)),(m=+-[3\sqrt{6}]/8 (t//m)):}`
Vậy `m=+-[3\sqrt{6}]/8`.

Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
![]()
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
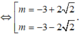
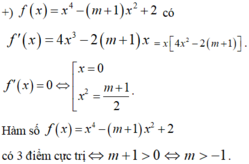
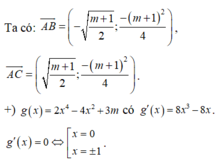

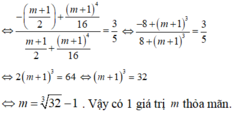




Chọn B
[Phương pháp tự luận]
Ta có y ' = 6 x 2 - 18 x + 12
A ( 1 ; 5 + m ) v à B ( 2 ; 4 + m ) là hai điểm cực trị của đồ thị hàm số
Chu vi của ∆ O A B là
Sử dụng tính chất u + v ≥ u + v
Từ đó ta có :
Dấu bằng xảy ra khi và chỉ khi u , v cùng hướng
Vậy chu vi ∆ O A B nhỏ nhất bằng ( 10 + 2 ) khi m = - 14 3