Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có y ' = 4 sin 2 x cos x sin x - ( 2 m 2 - 5 m + 2 ) cos x = cos x [ ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ]
Xét trên ( 0 ; π 2 ) ta thấy cos x > 0 , để hàm số đồng biến trên khoảng này thì ( 2 sin x - 1 ) 2 - ( 2 m 2 - 5 m + 3 ) ≥ 0 với ∀ x ∈ ( 0 ; π 2 ) hay ( 2 m 2 - 5 m + 3 ) ≤ 0 ⇒ 1 ≤ m ≤ 3 2 do m nguyên nên tồn tại duy nhất m=1

Chọn đáp án B.
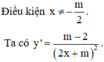
Hàm số đã cho đồng biến trên khoảng - ∞ ; - 8

Do đó, số tập con gồm 3 phần tử của tập hợp A là C 14 3 = 364



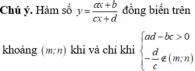

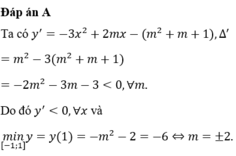

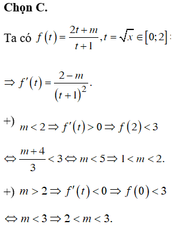
Đáp án C
Ta có y = 1 3 x 3 − m − 1 2 x 2 + m x + m − 1 ⇒ y ' = x 2 − m − 1 x + m ; ∀ x ∈ ℝ
Phương trình y ' = 0 ⇔ x 2 − m − 1 x + m = 0 *
Yêu cầu bài toán ⇔ * có 2 nghiệm phân biệt x 1 , x 2 thỏa mãn x 1 − x 2 = 1
⇔ Δ * > 0 x 1 − x 2 2 = 1 ⇔ m − 1 2 − 4 m > 0 x 1 + x 2 2 − 4 x 1 x 2 = 1 ⇔ m 2 − 6 m + 1 > 0 m − 1 2 − 4 m = 1 ⇔ m = 0 m = 6
Vậy số phần tử của tập S là 2