MA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MA
1
AH
Akai Haruma
Giáo viên
28 tháng 3 2022
Lời giải:
Đạo hàm \(y'=\frac{-1}{2\sqrt{4-x}}+\frac{1}{2\sqrt{4+x}}\)
Đoạn tìm đạo hàm tại $y'\geq 0$ ý bạn là gì nhỉ?
C
5 tháng 9 2016
a) \(y=\sqrt{1-sin\left(x^2\right)}-1\) đạt giá trị lớn nhất là 1 , giá trị nhỏ nhất là - 1 ( để ý rằng u = x + \(\frac{\pi}{3}\) lấy mọi giá trị thực tùy ý khi x thay đổi ) , nên hàm số y = 2cos \(\left(x+\frac{\pi}{3}\right)\) + 3 đạt giá trị lớn nhất là y = 2 . 1 + 3 = 5 , giá trị nhỏ nhất là y = 2 . ( - 1 ) + 3 = 1
b) Hàm số y = 4sin |x| = đạt giá trị lớn nhất là 4 ( khi sin | x | = 1 tức là | x | = \(\frac{\pi}{2}\) + 2k\(\pi\) , k nguyên không âm ) , đạt giá trị nhỏ nhất - 4 ( khi sin | x | = \(-\frac{\pi}{2}+2k\pi\) , k nguyên dương )
JE
1
HT
23 tháng 4 2021
\(y'=1+\dfrac{1}{2\sqrt{x^2+x}}\left(2x+1\right)\)
\(\Rightarrow xy'=x+\dfrac{2x^2+x}{2\sqrt{x^2+x}}>x+\sqrt{x+x^2}\)
\(\Leftrightarrow\dfrac{2x^2+x}{2\sqrt{x^2+x}}>\sqrt{x^2+x}\Leftrightarrow2x^2+x>2\left(x^2+x\right)\Leftrightarrow2x^2+x>2x^2+2x\Leftrightarrow x< 0\)
\(\Rightarrow S=\left(-\infty;0\right)\)
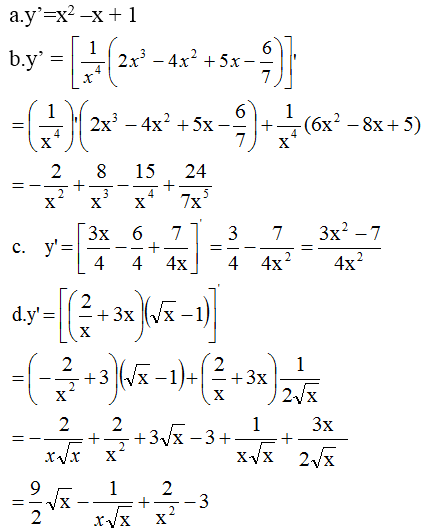
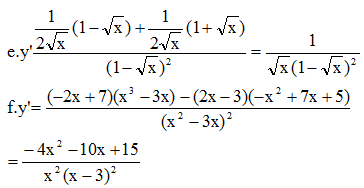
y' > 0 ⇔ \(\dfrac{-1}{2\sqrt{4-x}}+\dfrac{1}{2\sqrt{4+x}}>0\)
⇔ \(\dfrac{1}{2\sqrt{4+x}}>\dfrac{1}{2\sqrt{4-x}}\)
⇔ \(\dfrac{1}{\sqrt{4+x}}>\dfrac{1}{\sqrt{4-x}}\)
⇔ \(\left\{{}\begin{matrix}4-x>0\\4+x>0\\4+x< 4-x\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4-x>0\\4+x>0\\x< 0\end{matrix}\right.\) ⇔ -4 < x < 0.
Bạn thêm dấu = ở số 0 vào nhé